Chaotic dynamics in the kicked rotator problem

Kicker rotator (or rotor) problem is one of the classical examples of dynamical chaos in physics. The focus of this problem is a particle which moves in circular motion (e.g., pendulum on a stick). This particle is being acted upon periodically, lets assume that \( T=1 \), by homogeneous field (e.g., gravitational field, which is being turned on periodically for a brief periods of time). When the field is on, it creates a force, acting on the particle, of strength \( K \). As field is on only for a very brief periods of time, the force may be approximated by the Dirac delta function.

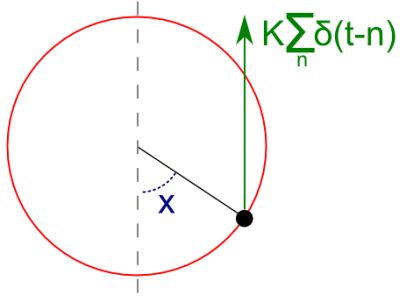Fig 1.General schema of kicked rotator.

The following Hamiltonian may be written for this system:

\begin{equation} \mathcal{H}[p(t),x(t),t] = \frac{p(t)^2}{2} + K\cos[x(t)] \sum_{n=-\infty}^{\infty} \delta(t-n) . \end{equation}

For anyone familiar with classical mechanics, it should be easy to obtain the following Hamiltonian equations (lets, for the sake of simplicity, assume that \( R=1 \) and \( m=1 \)):

\begin{equation} \partial_t \omega(t) = K \sin[x(t)]\sum_{n=-\infty}^{\infty} \delta(t-n) , \quad \partial_t x(t) =\omega(t) . \end{equation}

These equations maybe solved by noting that we have two distinct cases - one in which external force is absent, \( n < t < t' <n+1 \),

\begin{equation} \omega_{t'} = \omega_t , \quad x_{t'} = x_t + \omega_t(t' - t) , \end{equation}

and other in which external force is present, \( n <n+1-\varepsilon < t \lesssim t' < n+1+\varepsilon \) (\( \varepsilon \rightarrow +0 \)),

\begin{equation} \omega_{t'} = \omega_t + \Delta \omega , \quad x_{t'} =x_t + \omega_{t} (t' - t) , \end{equation}

\begin{equation} \Delta \omega = K\int_{n+1-\varepsilon}^{n+1+\varepsilon} \sin[x(t)]\delta(t-n-1) \mathrm{d} t = K \sin[x(n+1)] . \end{equation}

Thus analytical model may be well approximated by the following set of difference equations:

\begin{equation} x_{t+1} = ( x_t + \omega_{t}) \,\mathrm{mod}\, 2 \pi ,\quad \omega_{t+1} = \omega_t + K \sin(x_{t+1}) . \end{equation}

Here a pair of \( (x_t , \omega_t) \) describes particle's coordinate and radial speed (same magnitude as momentum) after \( t \)-th kick. A set of \( (x_t , \omega_t) \) curves for a given \( K \) and few distinct initial conditions, \( (x_0,\omega_0) \), is called Poincare plot. This plot gives basic insight into deterministic and chaotic dynamical behavior of the system.

Applet with two curves

In order to better understand the Poincare plot, one should start from a simple case with two curves. In the applet below we have selected two curves with extremely similar initial conditions, but qualitatively differing trajectories (one resonates with periodic force, while the other doesn't). Red ball starts with \( (x_0, \omega_0) \), while the initial conditions of blue ball are similar (in the applet below you may choose deviations from the initial conditions of red ball). Experiment with the default settings and also try some other sets of initial conditions. Note that you may also change the strength of the kicks, \( K \). Period of the external force was set to one second.

Many trajectory Poincare plot and Standard map

In the applet below you may study the Poincare plot of the kicked rotator with \( N_{trajectories} \) trajectories present. For the sake of simplicity the initial conditions of each trajectory are selected automatically - \( x_0 =\pi \) , \( \omega_0 =\frac{2 \pi i}{N_{trajectories}} \) (here \( i = 0, 1, \ldots,N_{trajectories} \)). Each trajectory is plotted until it becomes closed (some point is visited the second time) or until it has \( N_{max.points} \) points.

Note that for small \( K \) there are only few resonating trajectories - most of them circle single period point, \( (\pi,0) \), and two double period points - \( (0, \pi) \) and \( (\pi, \pi) \). As \( K \) increases (we encourage you to try \( 0.1 \), \( 0.5 \), \( 1 \), \( 1.5 \), \( 2 \) and \( 5 \)) number of resonant trajectories increases and the encircle more different period points (triple period, quadruple period and so on). With large values of \( K \) whole phase space of \( (x, \omega) \) is filled with resonant period points and trajectories become apparently random (chaotic as they are of deterministic nature).

Note that this applet allows to restrict \( \omega \) to the interval of \( (0, 2 \pi) \). From the physical system point of view, this makes no sense as both radial speed and momentum may obtain any value (indeed the values escape this range for larger values of \( K \)). Yet if \( \omega \) is restricted, then we obtain interesting case known as Standard, or Chirikov-Zaslavsky, map.