Edge redirection network formation models

Previously we wrote about few of the most well known and used network formation models [1]: Erdos-Renyi, Watts-Strogatz, Barabasi-Albert, core-periphery network and cellular network models. All these models are somewhat stylized and very simple - they are able to reproduce just some small part of actual complexity observed in the social networks. Thus it might be convenient to combine these models into hybrid network formation models, which then would be able to reproduce more empirically observed features.

One of the first steps away from the simple models and towards a more realistic models might be introduction of the local interactions. For example into the Barabasi-Albert model. Recall that in this model we had to keep track of the degrees of each node. But is it possible to have this information in real life? What would happen if we wouldn't have this information, but would explore the network through the random selection (just like in the Erdos-Renyi model)?

On the edge redirection networks

Wouldn't it be more natural to generate scale-free networks using a modified Erdos-Renyi model than the Barabasi-Albert model? Let us retain the purely uniform selection of the nodes of the original Erdos-Renyi model, but in contrast to the original we will select only one "old" node to connect to.

But not so fast! Let us with the probability \( r(a,b) \) to redirect the edge to the selected node's parent node (here \( a \) is a degree of the "old" target node and \( b \) is a degree of the parent node). Evidently the edge will not be redirected with the probability \( 1-r(a,b) \). We can now separate the redirection models into three groups (based on the asymptotic behavior of \( r(a,b) \)) - the hindered (if \( b \rightarrow \infty \), then \( r \rightarrow 0 \)), constant probability (\( r=\mathrm{const} \)) and enhanced (if \( b \rightarrow \infty \), then \( r \rightarrow 1 \)) redirection.

In case of the constant probability redirection we would obtain networks identical to the ones generated by the Barabasi-Albert modeli (\( \alpha=1 \)) [2, 3]. The hindered redirection case also provides networks which are similar to Barabasi-Albert model networks, but now with \( \alpha<1 \) [2]. The enhanced redirection case is a more interesting one - primarily, according to the authors, the network is non-extensive [3]. In this case we should also obtain a high dispersed network with multiple macro-hubs. [3] mentions that these kind of networks are observed in airline routes.

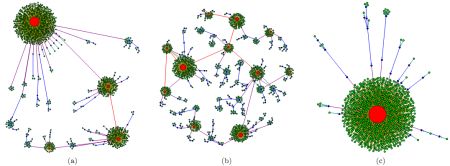Fig. 1:Highly dispersed networks shown in the article "Highly Dispersed Networks" by Gabel et al. (the enhanced redirection was used). The green nodes have a total degree of 1, blue nodes - have 2-20, while red ones - larger than 20.

Why are these models able to reproduce scale-free networks? Essentially it happens due to the fact that higher degree nodes are more probable to be selected as parent nodes, because of having more "routes" (child nodes) leading to them.

This is all that we can briefly tell you about the edge redirection network formation models. Note that this is only a brief introduction - there more papers available on this topic (e.g., see the list of references in [2, 3] papers).

Interactive applet

Using the interactive applet you can observe how the network is formed using edge redirection. Left panel of the applet shows the network itself, while in the right one you can observe how the degree probability density function evolves. Note that the probability density function plot is plotted on the lg-lg axes. Also note that the nodes in the left panel are colored based on their degree (if the degree equals 1, then they are green, if the degree is larger than 1, but smaller than 70% of largest degree, then they are blue, while in the other case they become red).

In case of enhanced redirection we choose the following form of \( r(a,b) \) (though note that it is not unique choice):

\begin{equation} r(a,b) = 1 - b^{-\lambda} . \end{equation}

In case of hindered redirection we chose that:

\begin{equation} r(a,b) = b^{-\lambda} . \end{equation}

While in case of constant probability redirection we set that \( r(a,b) = \lambda \).

Note that with a large number of nodes (100 or more) the applet might freeze and disrupt your browser operation, thus you should handle the applet with care. If you would like to analyze or generate large network consider downloading Gephi or obtaining other similar software packages.

References

• E. M. Airoldi, X. Bai, K. M. Carley. Network sampling and classification: An investigation of network model representations. Decision Support Systems 51: 506-518 (2011). doi: 10.1016/j.dss.2011.02.014.
• A. Gabel, S. Redner. Sublinear but never superlinear preferential attachment by local network growth. Journal of Statistical Mechanics 2013: P02043 (2013). doi: 10.1088/1742-5468/2013/02/P02043. arXiv: 1212.0518 [cond-mat.stat-mech].
• A. Gabel, P. L. Krapivsky, S. Redner. Highly Dispersed Networks. Physical Review E 88: 050802 (2013). doi: 10.1103/PhysRevE.88.050802. arXiv: 1307.3768 [cond-mat.stat-mech].