Sierpinski triangle

Sierpinski triangle is a fractal named after Polish mathematician Waclaw Sierpinski, who was the first one to describe it in scientific literature (in 1915). The fractal itself is interesting in a sense that it is a two dimensional attractor to couple iterative operations related to triangles (primarily).

In this text we will discuss iterative removal of triangles, shrinking and duplication, chaos game. We will also briefly mention Lindenmayer system, cellular automata and Pascal's triangles.

Iterative removal of triangles

Iterative removal of triangles is the main Sierpinski triangle construction algorithm and it is formulated as:

1. Let us start with an equilateral triangle.
2. Subdivide it into four smaller congruent equilateral triangles.
3. Remove the central smaller triangle - leave only ones on the sides.
4. Repeat steps 2 and 3 with each of the remaining smaller triangles.

Observe this algorithm in HTML5 app below. Using buttons "+" and "-" you can influence the maximal precision (recursive depth) in which the fractal is drawn. Observe self-similarity of the structure.

Shrinking and duplication

Alternatively you could do the following:

1. Choose any geometric object. There is no need to choose equilateral triangle.
2. Shrink it two times and make three copies of it. Two copies should form a base, while the third should be placed on top.
3. Repeat step 2 with all three copies.

Observe this algorithm in HTML5 app below. Once again use buttons "+" and "-" to influence the maximal precision (recursive depth) in which the fractal is drawn. Observe how a square starts to look like Sierpinski triangle.

Chaos game

This case is slightly more interesting as it is no longer deterministic - the actions in this "game" are chosen at random. The only definite thing is three main points. The algorithm itself is formulated as:

1. Choose three points, which could be connected to form a triangle. There is no need to connect them. Let us call them main points.
2. Choose a random point inside the triangle. Mark this point. Let us call it current position.
3. Select randomly any of the three main points.
4. Find a mid-point between the current position and selected main point. Mark this point. This point is our new current position.
5. Repeat steps 3-4 with the new current positions.

In the HTML5 app below we have show the main points as larger squares colored in three colors - red, green and blue. These colors are used when select color for the marking of the new current position (step 4). Note that colors stay separated and are near the appropriate main point.

Other ways to obtain Sierpinski triangle

One of the methods, previously discussed on Physics of Risk, to obtain Sierpinski triangle is cellular automata, Wolfram's elementary automatons. Rules 60 and 102 generate right Sierpinski triangles, while rule 90 generates ordinary Sierpinski triangle.

Fig. 1:Sierpinski triangle and elementary cellular automatons - 102, 90 and 60 rules.

Two more ways to obtain Sierpinski triangle are related to the Lindenmayer system. One is related to the arrowhead curve, which in this system is described as:

Initial condition: A, Angle: 60 deg, Rules: A -> B-A-B, B -> A+B+A.

While the other is related to the direct implementation of the borders in Sierpinski triangle:

Initial condition: AB-AA-AA, Angle: 120 deg, Rules: A -> AA, B -> -AB+AB+AB-AA.

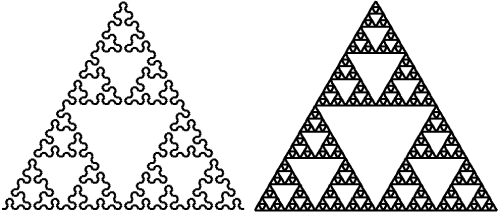Fig. 2:Sierpinski triangle and Lindenmayer system - arrowhead curve and direct implementation.

Finally the last method, considered in this text, is related to the Pascal's triangle. You should simply color cells with odd numbers black.

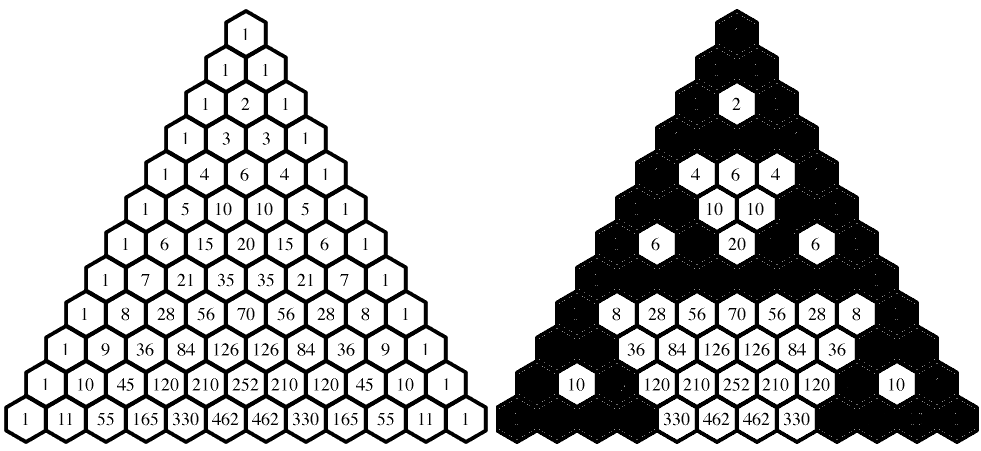Fig. 3:Sierpinski triangle and Pascal triangle