Colors of Noise

What is white, pink, "brown" and even black? It is around us every day and usually is very useful. Yet from time to time it annoys us and sometimes we even call police to keep it in check? The answer to this quite complex, as it is oriented towards people with physics background, question is unbelievably simple. Noise possesses all of the aforementioned qualities!

White noise was named after white color. As it should be known white color is actually a mixture of many different colors. Human sees it if all three color receptors in his eyes are equally stimulated. Equal stimulation usually means that the three main colors are of equal intensity or in physics language - spectral density is flat. Putting it more generally and simply - white noise is purely random, uncorrelated, noise - each new intensity value doesn't depend on any of the previous signal intensity values. The simplest example for the white noise could simple time series constructed by rolling six sided board game dice.

The essence of the "brown" noise also lies in its name, but unlike white noise the name is not related to the name of certain color. It is related to the Scottish botanist Robert Brown. In 1827 he observed pollen under the microscope and noticed that pollen move! Initially he thought that they were moving, because they are alive. Later he observed the same behavior by the clearly inanimate objects (ex., grains of iron), thus disapproving initial hypothesis. Though he was not able to find the reason for the observed movement. Only in the begging of 20th century mathematician Bachelier (1900) and physicist Einstein (1905) and Smoluchowski (1906) independently discovered reasons for this kind of movement. From the physical point of view pollen have moved due to many minute interactions with atoms and molecules, while in economical field Bachelier assumed that price moves because of random nature of incoming exogenous news. One can put this ideas more simply by saying that "brown" noise is an integral (or sum in discrete case) of the white noise. Thus the "brown" noise is strongly correlated - new intensity value strongly depends on the previous signal intensity value. Spectral density of such noise is of \( S(f) \sim 1/f^\beta \) type with the exponent equal to 2.

The last of the main colors of noise is pink. In Physics of Risk, and in the scientific literature, this type of noise is called flicker or 1/f noise. This is due to the spectral density of such noise, which is of \( S(f) \sim1/f^\beta \) type with exponent equal or approximately equal to 1. This noise is of great importance not only because it is in between of two easily physically understood white and brown noises, but also it is very common in complex and social systems. This type of noise is also rather pleasant to human ear, thus it is not so surprising that this type of noise is observed in many classical music pieces. It is thought that pink noise is pleasant due to the nature of human hearing. Human ear is used to "hear" sounds grouped by octaves, not frequencies, thus it is more pleasant to hear equally intense octaves, not frequencies (as in white noise). While 1/f spectral density function means that pink noise has equal power distributed over octaves (namely in case of pink noise 80-90 Hz octave would have approximately the same intensity as 800-900 Hz octave).

The colors of noise may be also illustrated with another very simple example. One can imagine white noise as a composition created by randomly pressing keys on the piano keyboard. Brown noise could be produced by a cat slowly walking over the same keyboard. For a pink noise we would additionally need a fly, which would be chase by a cat. At some points of time a cat would stay in approximately same place (pressing the same note repeatedly), while at other moments cat would jump towards a fly in order to catch it. Thus we would have very similar sounds and very distinct sounds grouped together.

You can also compare these type of noise by listening to them on playnoise.com website (edit: no longer available).

Qualities of different types of noise might be efficiently illustrated graphical. This is done in Fig. 1.

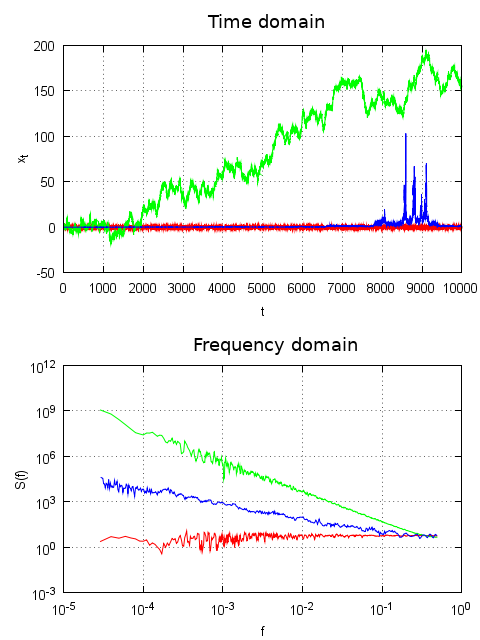Fig. 1:White (red curve), 'brown' (green) and pink (blue) noise time series and spectral densities.

Black noise is not an "official" type of noise. Silence is frequently colored this way. Also sometimes a noise with the spectral density of \( S(f) \sim 1/f^\beta \) type with the exponent larger than 2 is also considered black.

In the literature one can also find red, orange and green noise colors, but they have not widely acknowledged meanings or are the slightly modified versions of the four main types of noise.