Obtaining surface area using Monte Carlo method

Imagine that you have to measure the surface area of the lake by using only a cannon! Let us assume that the geometric shape of the lake is too complex to be dealt with using simple formulas and that you have almost infinite supply of cannon balls. In such case you just have to hope that you are perfectly random shooter! Why so?

If your shots cover the hitting area of the cannon uniformly then you can obtain the area of the lake by estimating the probability to hit it:

\begin{equation} S_{fig} = p S_{hit} , \end{equation}

here \( S_{fig} \) is an estimate of the surface area of certain geometric shape (lake for example), \( p \) is an estimate of the probability to hit the shape, while \( S_{hit} \) is the hitting area of the cannon. The obtained are of course will be only approximate, but one can arrive reasonably near the actual answer.

Next we illustrate this method by applying it towards three geometric shapes - square, circle and Euclidean egg. Why the Euclidean egg? Well, there are numerous reasons for it, one of them being Easter. Happy Easter!

Unit square

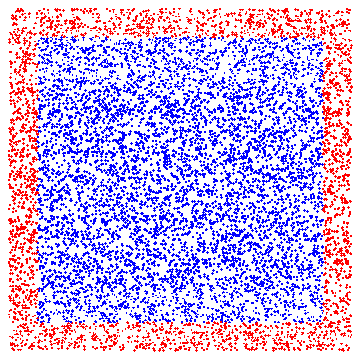Fig. 1:Random Monte Carlo

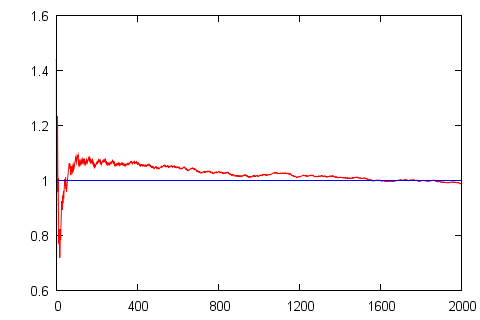Fig. 2:The evolution of guessed surface area (red curve) versus actual area (blue line).

Unit circle (estimation of the pi value)

It should be evident that the area of unit circle is equal to pi. Thus this case might also serve as pi value estimator.

Fig. 3:Random Monte Carlo

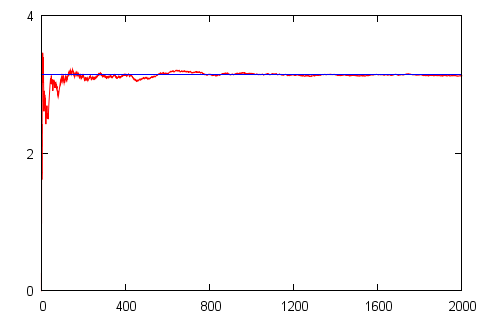Fig. 4:The evolution of guessed surface area (red curve) versus actual area (blue line).

Euclidean egg

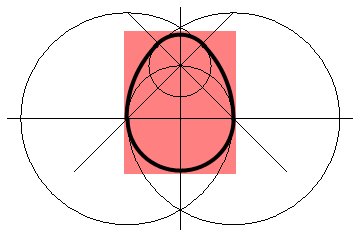Fig. 5:Full scheme for the definition of the Euclidean egg (the egg itself is inside the pink rectangle). The main part of the egg consists of the circle in the middle of the graph (its radius is equals 2). This egg is inside two larger circles, centers of which are on the sides, with radius 4. While the smallest circle closes up the egg from the top (its center lies on (0,2)).

In Fig. 5 you can see the Euclidean egg. The geometric shape is rather complex, but might be dealt with if you have decent skill in geometry. Thus the process might be still rather confusing:

\begin{equation} S_{fig} = \frac{\pi}{4} (4-2\sqrt{2})^2 + \frac{\pi}{8}4^2 + \frac{\pi}{2} 2^2 + \frac{\pi}{8} 4^2 - \frac{1}{2} 4\cdot 2 \approx 15.93 . \end{equation}

While be using the aforementioned method we can rather easily obtain the answer very close to the precise one. See Fig. 6 and Fig. 7 on the application of the Monte Carlo method in this case.

Fig. 6:Random Monte Carlo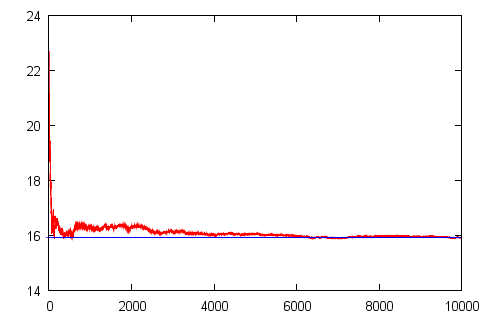

Fig. 7:The evolution of guessed surface area (red curve) versus actual area (blue line).