Polled voter model
We have already seen the basic workings of the poll-delayed voter model introduced in [1]. Previously, we have assumed that polling information is being revealed with delay and that the delay coincides with the polling period. However, quite often, processing polling information does not take a lot of time, so the information becomes available almost immediately. So, what changes when we remove this delay?
Model
The overall framework and the general form of the rates remain the same as discussed in the previous post. Yet there is an important difference, the rates now involve the outcome of the most recent poll, \( A_k \), instead of an earlier poll, \( A_{k-1} \). I.e.:
\begin{equation} \lambda_{k}^{+}=\left(N-X\right)\left[\varepsilon_{1}+A_k\right], \end{equation}
\begin{equation} \lambda_{k}^{-}=X\left[\varepsilon_{0}+\left(N-A_k\right)\right]. \end{equation}
So, effectively, the information delay still exists, but it only exists because information is updated periodically instead of continuously. With this kind of delay, periodic oscillations mostly disappear. For longer polling periods, one can observe the time series oscillating around the previous poll result. Usually, the new poll result is only marginally different from the prior outcome (within the natural variance of the process). These differences are not amplified, as was the case with the poll-delayed voter model when the information updates are delayed.
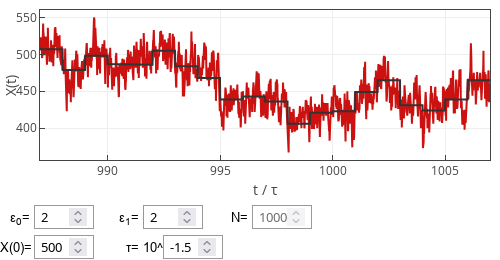Fig. 1:Sample trajectory of the polled voter model.Interactive app
This app is almost identical to the app from the previous post. The only difference is that this particular model does not require specifying two boundary conditions, specifying \( X_0 \) is sufficient.
Observe that this model does not exhibit emergent periodic oscillations. Note that for the shorter polling periods \( X(t) \) does not seem to follow \( A_k \) series. Instead, vice versa appears to be true. Also, in this regime, the changes in consecutive poll outcomes seem to be larger. While as the polling period becomes longer, \( X(t) \) starts to fluctuate around the \( A_k \). Thus, in this regime, the changes between the consecutive poll outcomes become small.
References
- A. Kononovicius, R. Astrauskas, M. Radavičius, F. Ivanauskas. Delayed interactions in the noisy voter model through the periodic polling mechanism. Physica A 652: 130062 (2024). doi: 10.1016/j.physa.2024.130062. arXiv:2403.10277 [physics.soc-ph].
