Strategic candidates and median voter theorem

Usually in sociophysics we care about the social aspects of opinion dynamics and ignoring grains of rationality present in decision making. Though there are models, which do the opposite. Here in this post we will take a look at a model [1] which considers rational voters and strategic candidates.

Model

In this model, unlike in the many iterations of the voter model, voters are abstracted away - they are represented by a population density function (black curve in the figures and the app). The function is given by a sum of two bell shapes (PDFs of the normal distribution):

\begin{equation} n(x) = c \left[ \mathcal{N}\left(x, \frac{1 + \alpha}{2}, \sigma^2 \right) + \mathcal{N}\left(x, \frac{1 - \alpha}{2}, \sigma^2 \right) \right] , \quad \text{if } x \in \left[ 0, 1 \right] . \end{equation}

In the above we have used \( \mathcal{N}\left(x, \mu, \sigma^2 \right) \) to indicate PDF of the normal distribution, while \( c \) is a normalization constant.

These generalized voters have four options: support blue candidate, support red candidate, support third party (extremists) or abstain. Utility of each choice is given by:

\begin{equation} U_B(x) = \frac{1}{|b-x|^P} , \quad U_R(x) = \frac{1}{|r-x|^P} , \end{equation}

\begin{equation} U_3(x) = \frac{1}{(1-x)^R} + \frac{1}{x^R} , \end{equation}

\begin{equation} U_A(x) = Q \left[ 1 - \left| |b-x| - |r-x| \right| \right]. \end{equation}

In the above \( b \) and \( r \) are the coordinates of blue and red candidate respectively. \( P \) stands for pragmatism (appeal to vote for mainstream candidate who is more likely to win). \( R \) stands for rebelliousness. \( Q \) could be interpreted as relative cost of voting, as higher values deter voters from voting if mainstream candidates (red and blue) are too alike.

Though the decision itself is not deterministic. Instead it is stochastic, but the grain of rationality is retained due to the probabilities being proportional to the respective utilities. E.g., probability to vote for a blue candidate is given by:

\begin{equation} p_B(x) = \frac{U_B(x)}{U_B(x) + U_R(x) + U_3(x) + U_A(x)} . \end{equation}

Note that red and blue curves (in the figures and the app) show the actual number of the red and blue candidates supporters. E.g., number of red candidate supporters is given by:

\begin{equation} n_R(x) = p_R(x) n(x) . \end{equation}

In other words candidates strategize about the expected vote share. Trivial stochasticity originating from Bernoulli trials is ignored at the vote count, too.

So the article [1] introducing this setup has looked at optimal positions for the candidates and shown that in some cases voter share maximizing (rational) candidates will become more radical than majority of their support base. For example try entering the following parameters into the interactive app below: \( \alpha = 0.6 \), \( \sigma = 0.1 \), \( P = 5 \), \( Q = 0 \) and \( R = 5 \).

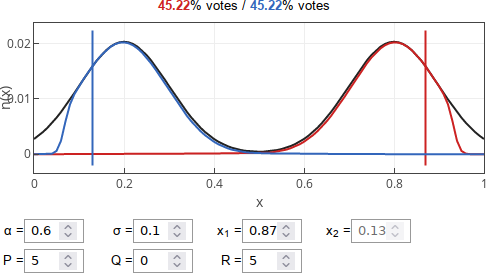Fig 1.In this case candidates (vertical lines) become more polarized than the society electing them.

Though for other parameter sets candidates will move closer towards the median voter. Such convergence is predicted by the Hotelling law and the median voter theorem. For example try: \( \alpha = 0.4 \), \( \sigma = 0.3 \), \( P = 2 \), \( Q = 30 \) and \( R = 1 \).

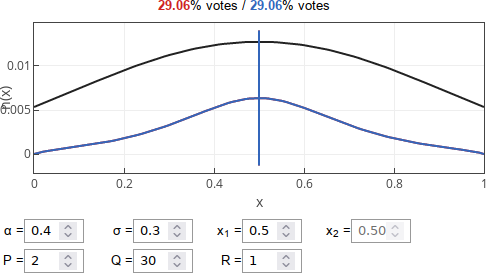Fig 2.In this case candidates (vertical lines) converge towards the median opinion.

In the intermediate phase candidates will be polarized, but less than the underlying society. This phase can be seen with the default parameters of the interactive app.

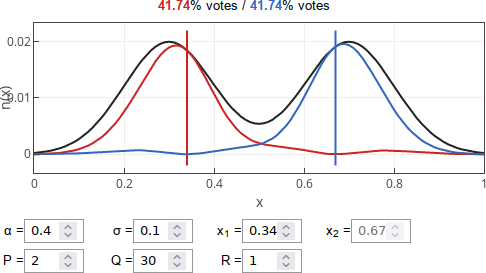Fig 3.The optimal positioning of the candidates (vertical lines) with the default parameter values. Candidates are polarized, but less than the society.

The authors of [1] also took a look at empirical distributions of voters and it seems that in the US scenario optimal strategic candidates should be less polarized than the US society itself. This seems to be a good news, but, sadly, we do not live in a rational world.

Interactive app

Note that interactive app requires you to play the game too. While the blue candidate is governed by a simple AI script, it is your responsibility to help the red candidate pick best "stance" on pressing political issues (\( x_1 \) value). While victory is not possible (as the setup is intentionally symmetric), but you achieve a draw. Feel free to experiment and find optimal position.

References

• M. I. Jones, A. D. Sirianni, F. Fu. Polarization, abstention, and the median voter theorem. arXiv: 2103.12847 [physics.soc-ph].