Supportive interactions in the noisy voter model preventing recruitment

Typically voter models assume that recruitment occurs between two interacting individuals. Obviously recruitment can occur only if these individuals have different opinions. While nothing will happen if these individuals hold the same opinions. Though Latane social impact [1] predicts that support provided by like-minded individuals can also play a role.

In a previous post we have consider the case when support prevents both recruitment and independent transitions. This needs not to be the case if we assume that independent transitions are not influenced by the support provided by the peers. This yields another variation of the noisy voter model with supportive interactions, which exhibits a more complicated phase portrait. This model is also a part of my last paper of the postdoctoral project [2].

The model

Let the agent in the same state provide support to each other and thus discourage switching away from the current state. Though let this support counter only recruitment by the agents with different opinions:

\begin{equation} \lambda^{+} \left(X\right)=\left(N-X\right)\left(\sigma_{1}+\left[\frac{h}{N^{\alpha}}X-\frac{q}{N^{\beta}}\left(N-X\right)\right]_{+}\right), \end{equation}

\begin{equation} \lambda^{-} \left(X\right)=X\left(\sigma_{0}+\left[\frac{h}{N^{\alpha}}\left(N-X\right)-\frac{q}{N^{\beta}}X\right]_{+}\right). \end{equation}

These are similar to the transition rates seen in the previous post. The only difference is that the independent transition rates are outside the special brackets, which enforce non-negativity. Other parameters retain their usual meaning: \( h \) represents recruitment (herding) rate, \( X \) corresponds to the number of agents in the first state and \( N \) is the total number of agents. With \( \alpha = 0 \), the model is non-extensive (i.e., it has a broad stationary distribution for any \( N \)). With \( \alpha = 1 \), the model is extensive (i.e., it has a narrow stationary distribution, which shrinks as \( N \rightarrow \infty \). Parameter \( \beta \) has similar meaning as \( \alpha \), but applies only to supportive interactions.

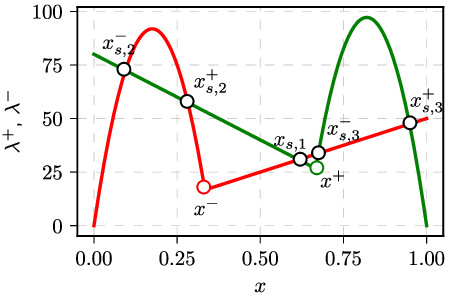Fig. 1:Special points of the transition rates (corresponds to Fig. 3 from the article).

Bifurcation diagrams of this model will be a bit more complicated as few different attraction basins exist (as can be seen in the figure above as well as Fig. 3 in [2]). The most important points are the roots of the special brackets:

\begin{equation} x^{+} = \frac{N^\alpha q}{N^\beta h + N^\alpha q} , \end{equation}

\begin{equation} x^{-} = \frac{N^\beta h}{N^\beta h + N^\alpha q} . \end{equation}

All of the fixed points (four of them) can be categorized in relation to the roots of the special brackets. Fixed point of the first type is observed in the region where both special brackets evaluate to zero, \( x^{-} < x_{s,1} < x^{+} \). In this region dynamics is dominated by independent behavior. The stationary point in this case will be found at:

\begin{equation} x_{s,1} = \frac{\sigma_1}{\sigma_0 + \sigma_1} . \end{equation}

Fixed points of the second and third types are found whenever only one the special brackets evaluates to zero. Fixed point of the second type will be observed if \( x_{s,2}^{\pm} < x^{+} \) and \( x_{s,2}^{\pm} < x^{-} \). While fixed point of the third type will be observed if \( x_{s,3}^{\pm} > x^{+} \) and \( x_{s,3}^{\pm} > x^{-} \). In these cases only one of the states is being protected by the supportive interactions. Stationary points will be found at:

\begin{equation} x_{s,2}^{\pm} =\frac{A\pm\sqrt{A^{2}-2B\sigma_{1}}}{B}, \end{equation}

\begin{equation} x_{s,3}^{\pm} =\frac{A+2\left(N^{1-\beta}q-\sigma_{0}-\sigma_{1}\right)\pm\sqrt{A^{2}-2B\sigma_{0}}}{B}. \end{equation}

In the above we have we have introduced convenient shorthands for the commonly repeated expressions:

\begin{equation} A=N^{1-\alpha}h+\sigma_{0}+\sigma_{1},\quad B=2N\left(N^{-\alpha}h+N^{-\beta}q\right). \end{equation}

Fixed point of the fourth type will be observed if for some \( x \) both of the special brackets evaluate to a positive number, \( x^{+} < x_{s,4} < x^{-} \). This implies that we can't observe fixed points of the first and fourth types at the same time. Though we can observe fixed points of the second or third type together with either of them. Stationary point can be observed at:

\begin{equation} x_{s,4}=\frac{Nq-N^{\beta}\sigma_{1}}{2Nq-N^{\beta}\left(\sigma_{0}+\sigma_{1}\right)}. \end{equation}

Determining critical values of \( q \) at which the phase transition occur in general case is troublesome analytically, but quite possible numerically for the specific parameter values. Below you should see a typical bifurcation diagram of the model (figure corresponds to Fig. 6 (b) from [2]).

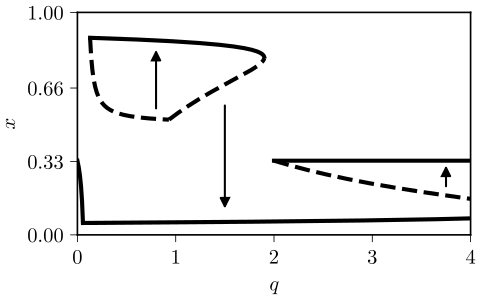Fig. 2:Bifurcation diagram of the model with α=β=0 (corresponds to Fig. 6 (b) from the article).

Interactive app

Use the app below to explore the phases of the noisy voter model with supportive interactions. As in the previous post this app also shows you the time series plot (on the left) and the rate plot (right). Time series plot show \( 10 \) sample trajectories, so that you could where different trajectories tend to. Rate plot shows to curves, red curve corresponds to death rate, while green curve corresponds to birth rate. Rate plot allows to anticipate where the stationary points will be and whether they will be stable. In most cases the model will converge towards stable stationary points, so here we neglect the usual statistical analysis, but we will revisit it in a later post

Acknowledgment. This post was written while reviewing literature relevant to the planned activities in postdoctoral fellowship ''Physical modeling of order-book and opinion dynamics'' (09.3.3-LMT-K-712-02-0026) project. The fellowship is funded by the European Social Fund under the No 09.3.3-LMT-K-712 ''Development of Competences of Scientists, other Researchers and Students through Practical Research Activities'' measure.

References

• B. Latane. The psychology of social impact. American Psychologist 36: 343-356 (1981). doi: 10.1037/0003-066X.36.4.343.
• A. Kononovicius. Supportive interactions in the noisy voter model. Chaos, Solitons and Fractals 141: 110627 (2021). doi: 10.1016/j.chaos.2020.110627. arXiv:2001.11066 [physics.soc-ph].