"Hidden" noisy voter model for the parliamentary presence

In an earlier post we have defined the parliamentary presence and shown that the data from Brazilian and Lithuanian parliaments exhibits anomalous diffusion. Actually we have analyzed Lithuanian data [1], while Brazilian data was considered by Vieira and others [2]. Also in a follow up post we have shown that a noisy voter model is able to reproduce ballistic regime and normal diffusion when we consider individual agent trajectories. Now let us extend the model to account for sub-linear diffusion of parliamentary attendance.

The model extension

Now let us assume that the attendance behavior is imperfect. Namely, agents in state \( 1 \) some times do not attend, while agents in state \( 0 \) do. Let \( q_i \) be the probability that agent in state \( i \) will attend the session. To keep the original meaning of states we have to require that \( q_0 \leq q_1 \).

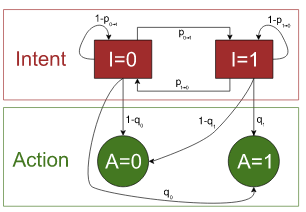Fig 1.(figure from my paper) Schematic representation of the hidden model

Note that this model is somewhat alike hidden Markov models, but the dynamics are assumed to be conditioned on the true (unobserved) state.

Now this small modification of the model allows us to recreate sub-linear diffusion. The exact dependence of power-law coefficient on \( q_i \) is not known, but by utilizing simulated annealing we were able to find parameter values for which the model replicates the empirically observed behavior of the Lithuanian Seimas [1]. These parameter values are the defaults of the app below.

The interactive app

Feel free to explore the model in the interactive app below. The upper plot shows how the attendance of the individual agents, \( N = 100 \), evolves within the window of 250 days, \( N_s = 250 \). Agent index varies on the y-axis, while time is on the x-axis. The lower left plot shows the cumulative presence series of three agents. The lower right plot shows the scaling law and standard deviation series for the data within the window of 250 days. Try varying model parameters to see how the law and the dynamics of the model change.

Acknowledgment. This post was written while reviewing literature relevant to the planned activities in postdoctoral fellowship ''Physical modeling of order-book and opinion dynamics'' (09.3.3-LMT-K-712-02-0026) project. The fellowship is funded by the European Social Fund under the No 09.3.3-LMT-K-712 ''Development of Competences of Scientists, other Researchers and Students through Practical Research Activities'' measure.

References

• A. Kononovicius. Noisy voter model for the anomalous diffusion of parliamentary presence. Journal of Statistical Mechanics 2020: 063405 (2020). doi: 10.1088/1742-5468/ab8c39. arXiv:2001.01479 [physics.soc-ph].
• D. S. Vieira, J. M. E. Riveros, M. Jauregui, R. S. Mendes. Anomalous diffusion behavior in parliamentary presence. Physical Review E 99: 042141 (2019). doi: 10.1103/PhysRevE.99.042141.