The illogical world - voting paradox

In the XVIII century Nicolas de Condorcet, French mathematician and philosopher, described an interesting situation, which is most widely known as the voting paradox. This situation is a perfect example of how the otherwise logical human behavior, on the individual level, can be easily destroyed by collective behavior, on the global level. We would naturally assume that the micro-level logic would rise bottom-up, yet it doesn't and that is a paradox!

Let us imagine that we have three persons who choose among three options. They are asked not choose a single of the available option, but they are asked to rank them according to their preference. Our aim is to understand the collective priorities of these three persons. For the sake of the simplicity let us assume that people have to choose between - apples, pear and cherry. The choice for each individual person should not be that hard and we would end up with three priority lists.

Now let us make assumptions about to of the lists. So, the first person likes apples more than bananas, while the cherries are in the third place. The second person is a cherry lover, while he likes apples and bananas less. After these two votes it is evident that apples are more likeable (3 of 4 cases), cherries are in the second place (2 of 4) and bananas are last (1 of 4). But let us not forget that we have a third person, who can ruin this perfect order. Indeed if he likes bananas over cherries over apples, then the priorities become mixed and illogical. From the voting table, it should be evident that apples (A) are liked more than bananas (B), while bananas are liked more than cherries (C), but the cherries are more liked than apples. The priority ordering becomes non-transitive:

\begin{equation} A > B > C >A . \end{equation}

Thus we have seen that people on the individual level had clear understanding of what the like the most, yet on the global level the community has no understanding of its preference. This situation is known as the voting paradox.

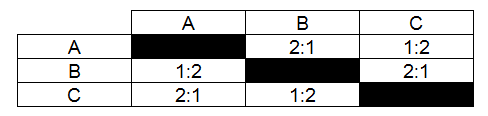Fig. 1:Voting table. A - apples, B - bananas, C - cherries.