Wolfram's elementary automatons
In mathematics and computation theory there are a class of cellular automatons which are known as elementary automatons. This class of cellular automatons is restricted to the one dimensional grid (in the figures below the second dimension, ordinate (vertical) axis, is time) with cells either on or off. Another important simplification is that the actual state of the cell at given time, \( x_{i,t} \), depends only on the previous state of the same cell and the previous states of its immediate neighbors, i.e., on \( \{x_{i-1,t-1},x_{i,t-1},x_{i+1,t-1}\} \). Due to these restrictions and simplifications, generally speaking cellular automatons might evolve in the infinite dimensions, have infinite neighborhoods and have limitless number of possible cell states, these cellular automatons appear to be very simple, though as we show below they can replicate very complex and even chaotic behavior.
These cellular automatons in some literature are named Wolfram's elementary programs as S. Wolfram was the first one who took up an interest in this kind of automatons. In his book "New Kind of Science" he notes that (differential) equations are unable to describe and fully explain some of the complex phenomena, while the world, be it nature or the Universe, itself loves elegant simplicity. Thus, as he claims, it is the best choice to look for the elementary laws behind the world and the elementary cellular automaton framework might be the one to provide interesting results. Actually as we show below this claim is at least partly true as even elementary cellular automatons might reproduce very complex and even chaotic behavior.
Describing the rules behind the elementary automaton
Recall that the cells of elementary cellular automaton might only be on or off. We also know that the future state of cell is defined by the states of three cells, itself and its immediate neighbors. So in order to introduce full description of the automaton's evolution we will need to defined eight distinct elementary, or neighborhood, rules. The requirement follows from the \( 2^3=8 \) (it covers all possible configurations). Thus there is a possibility of 256 rules describing global behavior, \( 2^8=256 \) (total number of all possible neighborhood rule configurations). One of the possible global rules is shown below in Fig. 1.
 Fig. 1:Rule 110 of elementary cellular automaton. In the first line you can see eight distinct sets of the initial conditions, i.e. all possible configurations of three neighborhood cells. On the second line you can see the set of eight possible results, each related to the condition drawn above them - empty cells in the second line means off, while cells with square inside mean that they will be on if the condition is met.
Fig. 1:Rule 110 of elementary cellular automaton. In the first line you can see eight distinct sets of the initial conditions, i.e. all possible configurations of three neighborhood cells. On the second line you can see the set of eight possible results, each related to the condition drawn above them - empty cells in the second line means off, while cells with square inside mean that they will be on if the condition is met.Note that the rule shown in Fig. 1 is known as rule 110. This notation, decimal number notation, is more comfortable than the full description as its shorter, more compact and more easily remembered. This number follows simply from the set of future configurations - just turn the on-off pattern into the binary number. The second line of Fig. 1 has the 01101110 on-off pattern. One can convert this binary number into the decimal like this:
\begin{equation} 0 \cdot 2^7 + 1 \cdot 2^6 + 1 \cdot 2^5 + 0 \cdot 2^4 +1 \cdot 2^3 + 1 \cdot 2^2 + 1 \cdot 2^1 + 0 \cdot 2^0 = 64 +32+8 +4 +2 = 110 . \end{equation}
In Fig. 2 we have shown how cellular automaton governed by the rule 110 evolves globally - what interesting structure it does posses. Fig. 3 is a close up on the Fig. 2 made in order to illustrate how the rule presented in Fig. 1 is applied in order to get the future generation of cells. Three distinct neighborhoods have been highlighted in Fig. 3 to show the agreement with rule 110, but feel free to study other neighborhoods to reassure yourself that shown cellular automaton indeed is governed by the rule 110.
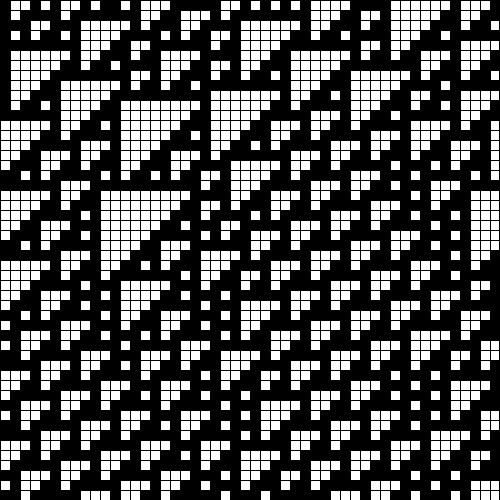 Fig. 2:Evolution of elementary cellular automaton governed by the rule 110. Initial condition is random set of cells. While evolution occurs in the cylinder space (the left and right edges are interconnected). Ordinate (vertical) axis is time axis - older generations are shown higher while younger ones are in the bottom.
Fig. 2:Evolution of elementary cellular automaton governed by the rule 110. Initial condition is random set of cells. While evolution occurs in the cylinder space (the left and right edges are interconnected). Ordinate (vertical) axis is time axis - older generations are shown higher while younger ones are in the bottom. Fig. 3:The close up on the two generations shown in Note that the highlighted neighborhoods (red squares) follow the rule 110. The red arrows point from the cells that influence the state to cell which is influenced by the states.
Fig. 3:The close up on the two generations shown in Note that the highlighted neighborhoods (red squares) follow the rule 110. The red arrows point from the cells that influence the state to cell which is influenced by the states.Other more interesting rules for the elementary cellular automaton
Not all of the 256 possible global rules provide interesting structures. Some the rules are trivial - they either disappear immediately or with some small oscillations dissipate towards some fixed structure. But there also are some interesting structures - periodic, chaotic and long lasting complex structures. In the table below you can see a list of some of the more interesting rules which we recommend to try using in the applet below.
| Rules | Structure if the input is one on-cell |
|---|---|
| 18, 22, 26, 82, 90, 126, 146, 150, 154, 182, 210, 218 | reminds of Sierpinsky triangle |
| 30, 50, 54, 58, 62, 86, 94, 114, 118, 122, 158,178, 186, 190, 214, 222, 242, 250, 254 | reminds of isosceles triangle |
| 28, 60, 70, 78, 102, 110, 124, 156, 188, 198, 296, 220, 230, 238 | reminds of right triangle |
Interactive applet
Usage of the applet is very simple - before doing actual evaluation you should input the rule and provide the first, input, generation of cells. Rule can be selected using the form show in Fig. 1 - just press mouse on the second line of cells in the form. First generation of cells might be also set using a mouse - just turn on or off the cells in the first line of the grid. If you do not want to provide first generation manually you can also press the button "Colonize" (the probability of on-cell might be set in the text field nearby). Next you can evaluate cellular automaton automatically (until the allocated grid ends) by using "Start" button. You can also evaluation generation one by one - just use the button "Iteration".
