Agent-based herding model of financial markets

Kirman's ant colony model, previously presented on our website as agent based (based on [1]) and stochastic (based on [2, 3]) model, has become classical example of herding modeling. Application of this model towards economic, financial or other social scenarios might seem doubtful as human society is far more complex than ant colony, but methodologically it is more useful to start from very simple and stylized model and later add complexity on top of it. Furthermore we have already shown that Kirman's herding dynamics could be applicable in agent-based marketing (see comparison of Kirman's and Bass diffusion model). In this text we will consider financial market scenario and obtain stochastic differential equations similar to the existing stochastic models considered in [4, 5].

Discussion and model presented in this text is the main topic of our paper on Microscopic reasoning for the non-linear stochastic models of long-range memory [6].

Introduction of variable event time scale

Original Kirman's model assumes constant agent meeting rate. In financial market scenario one could draw analogy between these events and trades, as trade is pair-wise interaction of traders, or agents in model's case, and also a great opportunity to reconsider available options. Thus we rewrite original one-step transition probabilities as

\begin{equation} p(X \rightarrow X+1)=(N-X) \left[\sigma_1 + \frac{hX}{\tau(X)} \right] \Delta t , \end{equation}

\begin{equation} p(X \rightarrow X-1)=X \frac{\sigma_2 + h (N-X)}{\tau(X)}\Delta t , \end{equation}

where \( \tau(X) \) is characteristic inter-event time, which now depends on system state. Note that in the above transition probabilities we have already assumed that one group of agent is rational, \( N-X \), while another is not, \( X \). For this reason transition rate, \( \sigma_1 \), of \( N-X \) has remained constant.

In this, more general, case derivation of stochastic differential equation in the manner it was done in [2] (also discussed on our website) is rather troublesome. Though alternatively we can use one-step process formalism [3, 7]. In such case we compactly express Master equation using one-step operators, \( \boldsymbol{E} \) and \( \boldsymbol{E}^{-1} \):

\begin{equation} \partial_t \omega(x,t) = N^2 \left\{ (\boldsymbol{E} -1)[ \pi^{-}(x) \omega(x,t) ] + (\boldsymbol{E}^{-1} -1) [\pi^{+}(x) \omega(x,t) ] \right\} , \label{master} \end{equation}

where \( \pi^{\pm}(x) \) are probability fluxes related to the transitions probabilities as \( P(X \rightarrow X \pm 1)=N^2 \pi^{\pm}(x) \Delta t \). Evidently \( x \) is continuous system state variable, defined as \( x= \frac{X}{N} \) (large \( N \) values can be assumed to secure continuity of the new system state variable).

As one-step operators act on continuous functions they can be expanded using Taylor series up to the second order terms:

\begin{equation} \boldsymbol{E}[f(x)] = f(x+\Delta x) \approx f(x) + \Delta x \partial_x f(x) + \frac{\Delta x^2}{2} \partial^2_x f(x) , \end{equation}

\begin{equation} \boldsymbol{E}^{-1}[f(x)] = f(x-\Delta x) \approx f(x) -\Delta x \partial_x f(x) + \frac{\Delta x^2}{2} \partial^2_xf(x) , \end{equation}

where \( \Delta x \) is smallest possible increment of the continuous system state variable, \( \frac{1}{N} \). After this expansion Master equation, Eq. \eqref{master}, becomes Fokker-Planck equation:

\begin{equation} \partial_t \omega(x,t) = -\partial_x [A(x) \omega(x,t)]+ \frac{1}{2} \partial^2_x [D(x) \omega(x,t)] , \label{fokpla} \end{equation}

where \( A(x) \) and \( D(x) \) are custom functions:

\begin{equation} A(x) = N (\pi^{+}(x)-\pi^{-}(x)) = \sigma_1 (1-x) -\frac{\sigma_2 x}{\tau(x)} , \end{equation}

\begin{equation} D(x) = \pi^{+}(x)+\pi^{-}(x) \approx \frac{2 h x(1-x)}{\tau(x)} . \end{equation}

The above Fokker-Planck equation, \eqref{fokpla}, can be rewritten as Langevin equation:

\begin{equation} \mathrm{d} x = A(x) \mathrm{d} t + \sqrt{D(x)} \mathrm{d} W= \left[ \sigma_1 (1-x) - \frac{\sigma_2 x}{\tau(x)} \right]\mathrm{d} t + \sqrt{\frac{2 h x (1-x)}{\tau(x)}} \mathrm{d} W . \end{equation}

To simplify model we can introduce dimensionless time, \( t_s = ht \):

\begin{equation} \mathrm{d} x = \left[ \varepsilon_1 (1-x) -\frac{\varepsilon_2 x}{\tau(x)} \right] \mathrm{d} t_s +\sqrt{\frac{2 x (1-x)}{\tau(x)}} \mathrm{d} W_s , \label{lanx} \end{equation}

where \( \varepsilon_i \) are accordingly rescaled original model parameters, \( \varepsilon_i = \frac{\sigma_i}{h} \).

Introducing price and return

While introducing variable time scale we assumed that there are at least two types of traders - some are rational, while some are not so. In recent agent-based modeling [8] it is also very common to assume that there are two types of traders in the market - fundamentalists and noise traders. By definition fundamentalists are assumed to be rational investors aiming for the long term profits, while noise traders rely on technical trading strategies aiming for short term profits.

Fundamentalists base their decision on information about the stock's value in the market. This information is quantified via so-called fundamental price, \( P_f(t) \). Fundamentalists expect that in long-run market will tend towards correct estimate of the stock's value. If \( P_f(t) > P(t) \) fundamentalists will expect growth of prices, thus placing buying orders. In the opposite case they'll attempt to sell stock, as they will expect decrease of price. These ideas are mathematical put down as [2]:

\begin{equation} D_f(t) = N_f(t) \ln \frac{P_f(t)}{P(t)} , \end{equation}

where \( D_f(t) \) is fundamentalists', \( N_f \) entities, excess demand at a given time.

Contrary noise traders attempt to forecast future prices based on previous price movements. As they are using price charts to make forecast, they are also called chartists. As very is a wide selection of very different chartist trading strategies, chartists are likely to make very different forecasts. Difference in forecasts would lead to difference in bids. This intrinsic disagreement might be macroscopically seen as irrational mood of noise traders. Thus theirs' excess demand can mathematical be expressed as [2]:

\begin{equation} D_c(t) = r_0 N_c(t) \xi(t) , \end{equation}

where \( \xi(t) \) is an average noise traders' mood, \( r_0 \) is scaling term, which might also be seen as relative impact of chartists' trades on the market.

Now one can use Walras law in order to obtain definition of price and, later, return. Original Walras law [9] assumes that trading in the market occurs trough the market maker, who stabilizes the market. Market is consider to be stable if all agents' excess demands equal zero:

\begin{equation} \sum_{i=1}^{N} D_i(t) = D_f(t) + D_c(t) = N_f(t) \ln\frac{P_f(t)}{P(t)} + r_0 N_c(t) \xi(t) = 0 , \end{equation}

\begin{equation} P(t) = P_f(t) \exp \left[ r_0 \frac{N_c(t)}{N_f(t)}\xi(t) \right] , \end{equation}

here one can assume that fundamental price remains constant (i.e., it is not a function of time). As we have definition of price, now we can obtain definition of return:

\begin{equation} r_{T}(t)=\ln \frac{P(t)}{P(t-T)} = r_0 \left[\frac{x(t)}{1-x(t)} \xi(t) - \frac{x(t-T)}{1-x(t-T)} \xi(t-T)\right] . \label{fullret} \end{equation}

Note that in the above we have expressed \( N_c(t) \) and \( N_f(t) \) using \( x(t) \), which we have defined previously as a systems state variable of Kirman's model. As fundamentalists are rational we have set that \( N_f(t)/N = 1-x(t) \), while chartists are thus directly related to \( x(t) \).

In [2] definition of return, \eqref{fullret} is simplified by using adiabatic approximation. Namely it is assumed that noise traders' change their mood very quickly, if compared with \( x(t) \). This gives simpler definition of return:

\begin{equation} r(t)=r_0 \frac{x(t)}{1-x(t)} \zeta(t) , \label{return} \end{equation}

where \( \zeta(t) \) is a change of noise traders' mood, \( \zeta(t) = \xi(t) - \xi(t-T) \). This change can be modeled in different ways, in [2] it is modeled using spin noise. In such case \( y(t)=\frac{x(t)}{1-x(t)} \) can be seen as absolute return, for which we will derive stochastic model in the next section of this text.

Derivation of stochastic model for absolute return, y

Eqs. \eqref{lanx} and \eqref{return} were derived in [2] (stochastic model was derived in a bit different way), but Alfarano et al. stopped there and did not derive stochastic differential equation for absolute return. In order to obtain stochastic model for absolute return we use variable substitution formula, via Ito's lemma, [10]:

\begin{equation} \mathrm{d} y(x) = \left[ A_x(x) \partial_x y(x) +\frac{1}{2} B_x^2(x) \partial^2_x y(x) \right] \mathrm{d} t +B_x(x) \partial_x y(x) \mathrm{d} W , \end{equation}

to obtain stochastic model for \( y \):

\begin{equation} \mathrm{d} y = \left(\varepsilon_1 + y\frac{2-\varepsilon_2}{\tau(y)} \right) (1 + y) \mathrm{d} t_s +\sqrt{\frac{2 y}{\tau(y)}} ( 1 + y ) \mathrm{d} W_s . \label{lany} \end{equation}

If we consider \( \tau(y) = y^{-\alpha} \), this selection might be backed by the positive correlation between trading activity and absolute return and also by the similarity of statistical properties, and a limit of large \( y \) values Eq. \eqref{lany} becomes:

\begin{equation} \mathrm{d} y = (2-\varepsilon_2) y^{2+\alpha} \mathrm{d}t_s + \sqrt{2 y^{3+\alpha}} \mathrm{d} W_s . \label{lanyour} \end{equation}

We find that Eq. \eqref{lanyour} is very similar to stochastic differential equation consider in [5]:

\begin{equation} \mathrm{d} y = \left( \eta - \frac{\lambda}{2} \right)y^{2 \eta -1} \mathrm{d} t + y^\eta \mathrm{d} W , \label{oursde} \end{equation}

which is known to give power law statistics:

\begin{equation} S(f) \sim \frac{1}{f^\beta}, \quad\beta=1+\frac{\lambda-3}{2(\eta-1)} , \end{equation}

\begin{equation} p(y) \sim y^{-\lambda} . \end{equation}

As relations between different model parameters are \( \eta =\frac{3+\alpha}{2} \), \( \lambda = \varepsilon_2 + \alpha+1 \) (obtained by directly comparing stochastic differential equations \eqref{lanyour} and \eqref{oursde}), we expect that \( y \) defined by Eq. \eqref{lany} will also have power law statistics:

\begin{equation} S(f) \sim \frac{1}{f^\beta}, \quad\beta=1+\frac{\varepsilon_2+\alpha-2}{1+\alpha} , \end{equation}

\begin{equation} p(y) \sim y^{-\varepsilon_2 - \alpha -1} . \end{equation}

Using these predictions we have reproduced \( 1/f \) noise in three distinct cases (see Fig 1., this figure is featured in [6]).

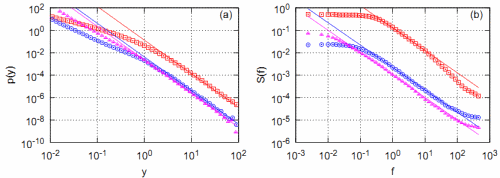Fig. 1:Numerically calculated PDF (a) and power spectral density (b) in three distinct cases, \( \alpha =0 \) (red squares), \( \alpha=1 \) (blue circles) and \( \alpha=2 \) (magenta triangles), of considered stochastic model, Eq. (6). Other model parameters were set as follows: \( \varepsilon_1=0 \), \( \varepsilon_2 =2-\alpha \). Solid curves are inverse power law fits: (a) \( \lambda=3 \) (all three cases), (b) \( \beta = 1 \) (all three cases).

The above comparison is very important as stochastic differential equation \eqref{oursde} is a more general case of our stochastic model of return [11]. Working on this approach further we might be able to create agent-based model providing more sophisticated statistical features reproduced by the model consider in [11].

There is another stochastic model whose stochastic differential equation resembles Eq. \eqref{lany}. It is so-called generalized CEV process, which was consider in [4]:

\begin{equation} \mathrm{d} y = a y \mathrm{d} t + b y^\eta \mathrm{d} W .\label{cev} \end{equation}

Eq. \eqref{cev} is noted to be a special case of Eq. \eqref{oursde}, when exponential diffusion restriction is applied [4]. Though comparison with generalized CEV process is important on its own, as generalized CEV process encompass many stochastic models used in risk management. In order to obtain similar stochastic differential equation we have to linearize drift function of Eq. \eqref{lany} (i.e. set \( \varepsilon_2 = 2 \)). Similarity is once again obtained in the limit of large \( y \) values:

\begin{equation} \mathrm{d} y = \varepsilon_1 y \mathrm{d} t_s + \sqrt{2y^{3+\alpha}} \mathrm{d} W_s . \end{equation}

Due to the similarity between Eqs. \eqref{oursde} and \eqref{cev}, theoretical predictions of statistical properties remain the same. Though now they have a bit simpler mathematical expression:

\begin{equation} S(f) \sim \frac{1}{f^\beta}, \quad\beta=1+\frac{\alpha}{1+\alpha} , \end{equation}

\begin{equation} p(y) \sim y^{- \alpha -3} . \end{equation}

In case of generalized CEV process we can't reproduce \( 1/f \) noise in three distinct cases, but we can still obtain three different power law spectral densities in three distinct cases (in each cases giving precise prediction). In Fig 2., this figure is featured in [6], we have shown that theoretical predictions for CEV process are also valid for \( y \) defined by Eq. \eqref{lany}.

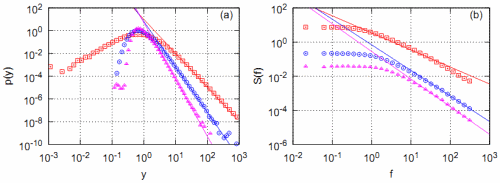Fig. 2:Numerically calculated PDF (a) and power spectral density (b) of considered stochastic model, Eq. (6), with linearized drift function in three distinct cases, \( \alpha=0 \) (red squares), \( \alpha=1 \) (blue circles) and \( \alpha=2 \) (magenta triangles). Other model parameters were set as follows: \( \varepsilon_1 = \varepsilon_2 =2 \). Solid curves provide inverse power law fits for modelic data: (a) \( \lambda=3 \) (red squares), \( \lambda=4 \) (blue circles), \( \lambda=5 \) (magenta triangles), (b) \( \beta=1 \) (red squares), \( \beta=1.5 \) (blue circles), \( \beta=1.66 \) (magenta triangles).

Applet

This applet numerically solves Eq. \eqref{lany} using Euler-Maruyama method [12]. In such case Eq. \eqref{lany} becomes a set of difference equations:

\begin{equation} y_{i+1} = y_i + \frac{\kappa^2}{1+y_i} \left[\frac{\varepsilon_1 y_i}{\tau(y_i)} + 2 - \varepsilon_2\right] + \kappa \sqrt{2} \varsigma_i , \end{equation}

\begin{equation} t_{i+1} = t_i + \frac{\kappa^2 \tau(y_i)}{y_i(1+y_i)^2} , \end{equation}

where \( \kappa \) is numerical precision parameter (numerical solution tends to improve with smaller values of the parameter (applet uses \( \kappa =0.4 \))), while \( \varsigma_i \) is normally distributed (zero mean, unit variance) random variable. Precision and quality of numerical results are also influenced by the enforced restrictions (in applet values of \( y \) are restricted in \( [0.01,100] \) value interval).

The applet plots both time series and statistical properties in real time. In the first few moments it may show incorrect and very approximate results - please wait a bit for a program to "settle down", it will start to show correct and precise results as time passes.

References

• A. P. Kirman. Ants, rationality and recruitment. Quarterly Journal of Economics 108: 137-156 (1993).
• S. Alfarano, T. Lux, F. Wagner. Estimation of Agent-Based Models: The Case of an Asymmetric Herding Model. Computational Economics 26: 19-49 (2005).
• S. Alfarano, T. Lux, F. Wagner. Time variation of higher moments in a financial market with heterogeneous agents: An analytical approach. Journal of Economic Dynamics and Control 32: 101-136 (2008).
• S. Reimann, V. Gontis, M. Alaburda. Interplay between positive feedback in the generalized CEV process. Physica A 390: 1393-1401 (2011). arXiv: 1008.0568 [physics.data-an].
• J. Ruseckas, B. Kaulakys. 1/f noise from nonlinear stochastic differential equations. Physical Review E 81: 031105 (2010). arXiv: 1002.4316 [nlin.AO].
• A. Kononovicius, V. Gontis. Agent based reasoning for the non-linear stochastic models of long-range memory. Physica A 391: 1309-1314 (2012). doi: 10.1016/j.physa.2011.08.061. arXiv: 1106.2685 [q-fin.ST].
• N. G. van Kampen. Stochastic process in Physics and Chemistry. North Holland, Amsterdam, 2007.
• M. Cristelli, L. Pietronero, A. Zaccaria. Critical Overview of Agent-Based Models for Economics. Proceedings of the School of Physics 'E. Fermi', Course CLXXVI, ed. F. Mallnace, H. E. Stanley, pp. 235-282. SIF-IOS, Bologna-Amsterdam, 2012. doi: 10.3254/978-1-61499-071-0-235.
• A. Jolink. The evolutionist economics of Lean Walras. Routledge, London and New York, 1996.
• C. W. Gardiner. Handbook of stochastic methods. Springer, Berlin, 2009.
• V. Gontis, J. Ruseckas, A. Kononovicius. A Non-linear Stochastic Model of Return in Financial Markets. In: Stochastic Control, ed. C. Myers. InTech, 2010. doi: 10.5772/9748.
• P. E. Kloeden, E. Platen. Numerical Solution of Stochastic Differential Equations. Springer, Berlin, 1999.