Stochastic ant colony model

Previously on Physics of Risk website we have presented Kirman's ant colony agent-based model [1], where each ant was represented as an agent. In this article we will move from the agent-based model framework to the stochastic differential equation framework. Thus showing that in case of simple agent-based models full transition to stochastic framework is possible. This transition is very important as stochastic framework is very popular and well developed in quantitative finance. The problem is that stochastic framework mainly gives only a macroscopic insight into the modeled system, while microscopic behavior currently is also of big interest.

Derivation of stochastic differential equation

In this section of the article we will follow derivation of stochastic differential equation, analogous to the previously discussed agent based model, done by Alfarano and Lux in [2]. Authors of [2] in their derivation follow the underlying ideas of birth-death processes or one-step processes, overview of which is given in most of handbooks concerning Stochastic Calculus. Thus if you want to get more familiar with the ideas below you should see [3] or other similar works.

Alfarano and Lux start by simplifying notation, used in the previous agent-based model, of system state, defined as number of ants using one of the food sources, \( X \), transition probabilities,

\begin{equation} p(X \rightarrow X+1) = \pi_{+}(X) \Delta t , \end{equation}

\begin{equation} p(X \rightarrow X-1) = \pi_{-}(X) \Delta t , \end{equation}

where \( \pi_{+}(X) \) stands for \( (N - X) (\sigma_1 + hX) \) and \( \pi_{-}(X) \) for \( X (\sigma_2 + h(N-X)) \). In such case Master equation, for very short times \( \Delta t \), can be expressed as

\begin{equation} \frac{\Delta \bar \omega_X}{\Delta t} = {\bar\omega_{X+1}} \pi_{-}(X+1) + {\bar \omega_{X-1}} \pi_{+}(X-1) -{\bar \omega_{X}} \pi_{-}(X) - {\bar \omega_{X}} \pi_{+}(X) , \end{equation}

here \( \bar \omega_X \) is probability for system to be in the state described by agent number \( X \), or in the other words probability of \( X \) ants at a given time to be using one of the two food sources.

It is comfortable for further derivation to introduce, from the Master equation above, total probability flux, \( \bar j_{i} \), between states \( X=i \) and \( X=i-1 \). Latter can be expressed as

\begin{equation} \bar j_{i} = \bar \omega_{i-1} \pi_{+} (i-1) - \bar\omega_{i} \pi_{-} (i) , \end{equation}

here first term describes transitions from \( X=i-1 \) to \( X=i \), while the second term describes transitions in the opposite direction - from \( X=i \) to \( X=i-1 \). Thus if flux, \( \bar j_{i} \), is positive system state with larger \( X \) becomes more probable than the system state with smaller \( X \). Now by using defined probability fluxes and Master equation above one can obtain a discrete continuity equation

\begin{equation} \frac{\Delta \bar \omega_X}{\Delta t} + \bar j_{X+1} -\bar j_{X} = 0 . \end{equation}

The interpretation of this equation is generally the same as, for example, in case of electric current continuity equation - if flux outside of current system state (or differential volume in case of electric current) is positive, the probability (analogous to charge) density of this system state will decrease. This idea stands behind the idea of local continuity. If probability flux vanishes at some boundaries, let say \( \bar j_0 = \bar j_{N+1} = 0 \), then one can show that \( \sum_i \bar \omega_i = 1 \) is true for every time moment. The last result actually stands behind the idea of the global continuity.

Now lets move on from the discrete case of \( X \in \{ 0,\,1,\, 2,\, \dots ,\, N \} \) to continuous case with \( x \in[0,\,1] \), applying transformation \( x= \frac{X}{N} \), where \( N \rightarrow \infty \). One can rewrite probability of continuous system state through discrete system state as

\begin{equation} \omega (x) = N \bar\omega_{x N} , \end{equation}

and total probability flux as

\begin{equation} j \left(x - \frac{1}{2 N} \right) = \bar j_{x N} . \end{equation}

The reasoning behind the offset in the latter equation lies within the fact that flux noted by \( \bar j_i \) connects two discrete states \( X=i-1 \) and \( X=i \), thus it should be located in the middle of that interval. This offset also helps to avoid tedious mathematics in further derivation. Alfarano and Lux also mention that this offset in flux is widely used in discretization of Maxwell's equations and in gauge theories on a discrete lattices (see the references in [2]).

One can rewrite the above discrete continuity equation in continuous terms by taking analogy with electric current continuity equation or by expanding \( j(x) \) using Taylor series expansion (dropping second order, \( N^{-2} \), and above terms). Either way one would obtain,

\begin{equation} \frac{\partial \omega (x)}{\partial t} + \frac{\partial j(x)}{\partial x} = 0 , \end{equation}

continuity equation for continuous time (is introduced by assuming that \( \Delta t \rightarrow 0 \)) and space.

Now let's recall definition of total probability flux in discrete terms and rewrite it in continuous terms. In the process it becomes

\begin{equation} j (x) = \frac{1}{N} \left[ \omega \left( x - \frac{1}{2N}\right) \pi_{+} \left(x N - \frac{1}{2} \right) - \omega \left(x + \frac{1}{2N} \right) \pi_{-} \left(x N + \frac{1}{2} \right)\right] . \end{equation}

In the equation above \( x \) was additionally shifted by \( \frac{1}{2 N} \).

When \( N \rightarrow \infty \), we can also expand \( \omega ( x \pm \frac{1}{2 N}) \), using Taylor series expansion (up to second order), as \( \omega(x) \pm \frac{1}{2 N} \partial_x\omega(x) \). And thus we finally obtain

\begin{equation} j(x) = \frac{\pi_{+}\left(x N - \frac{1}{2}\right) -\pi_{-}\left(x N + \frac{1}{2}\right)}{N} \omega(x) -\frac{\pi_{+}\left(x N - \frac{1}{2}\right) + \pi_{-}\left(x N+ \frac{1}{2}\right)}{2 N^2} \partial_x \omega(x) . \end{equation}

Now one should put into the equation above definitions of \( \pi_{+} \) and \( \pi_{-} \) to make one more step in derivation, but before this it is comfortable to define two custom functions

\begin{equation} D(x) = 2 h x (1-x) + \frac{\sigma_1 (1-x) + \sigma_2 x}{N}, \end{equation}

\begin{equation} A(x) = \sigma_1 (1-x) - \sigma_2 x . \end{equation}

Then after putting in definitions of transitions probabilities, \( \pi_{+} \) and \( \pi_{-} \), and dropping terms of second order and above one obtains

\begin{equation} j(x) = A(x) \omega(x) - \frac{1}{2}\frac{\partial}{\partial x} [ D(x) \omega(x) ] . \end{equation}

And then from continuity equation one can obtain Fokker-Plank equation

\begin{equation} \frac{\partial}{\partial t} \omega (x,t) = -\frac{\partial}{\partial x} [ A(x) \omega (x,t) ] + \frac{1}{2}\frac{\partial^2}{\partial x^2} [ D(x) \omega (x,t) ] , \end{equation}

which produces the same dynamics as agent-based model. Note that custom functions, which were introduced before, have special meaning - \( A(x) \) describes drift of the system state and \( D(x) \) describes its diffusion.

Fokker-Plank equation above can be alternatively modeled using Langevin stochastic differential equation (for general details on conversion see [3])

\begin{equation} \mathrm{d} x = A(x) \mathrm{d} t + \sqrt{D(x)} \mathrm{d} W, \end{equation}

and in the limit of high \( N \)

\begin{equation} \mathrm{d} x = \left[ \sigma_1 (1-x) - \sigma_2 x\right] \mathrm{d} t + \sqrt{2 h x (1-x)} \mathrm{d} W , \end{equation}

here \( W \) is Wiener-Brownian process. This, final, equation is solved in the java applet below.

Observed population fraction dynamics

The only thing, which has changed since the previous implementation of Kirman's ant colony model, is modeling framework - in the section above we have derived Langevin equation for Kirman's ant colony. Thus observations discussed in the previous article also apply towards this model. This time we just limit ourselves to simply showing that Langevin equation and agent-based model produce same results using same parameter values (see Fig 1.).

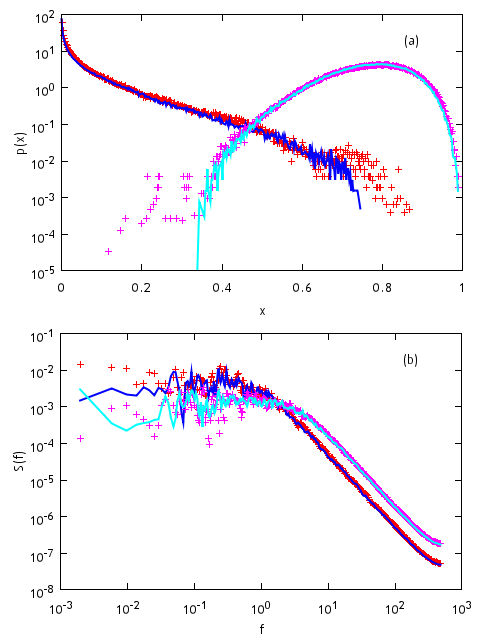Fig. 1:Comparison of probability density function (a) and power spectral density (b) of external observable, x, time series, which were produced by agent-based model (points) and stochastic model (lines). Parameters are set as follows: \( h=1 \) (same in all cases), \( \sigma_1 =0.2 \) (red points, blue lines), \( \sigma_1 =16 \) (magenta points, cyan lines), \( \sigma_2=5 \) (same in all cases).

Population fraction SDE Applet

In the applet below we solve aforementioned Langevin equation using simple Euler-Maruyama method (see [4]). Using this method we transform stochastic differential equation into difference equation

\begin{equation} x_{i+1} = x_{i} + \left[ \sigma_1 (1-x) - \sigma_2 x\right] \Delta t + \sqrt{2 h x (1-x) \Delta t} \zeta_i , \end{equation}

where \( \zeta_i \) is Gaussian random variable with zero mean and unit variance. As \( x \) has meaning only in the interval \( [0,\, 1] \), we also enforce boundary conditions to restrict \( x_i \) values.

References

• A. P. Kirman. Ants, rationality and recruitment. Quarterly Journal of Economics 108: 137-156 (1993).
• S. Alfarano, T. Lux, F. Wagner. Estimation of Agent-Based Models: The Case of an Asymmetric Herding Model. Computational Economics 26: 19-49 (2005).
• C. W. Gardiner. Handbook of stochastic methods. Springer, Berlin, 2009.
• P. E. Kloeden, E. Platen. Numerical Solution of Stochastic Differential Equations. Springer, Berlin, 1999.