Anomalous diffusion of the parliamentary presence data

While my postdoctoral project has already finished (actually it did finish almost a year ago), I still have things related to it I want to discuss here on Physics of Risk. This time let me take an empirical perspective, let me consider parliamentary presence data. Why this data could be interesting to us? Because, it was shown that parliamentary presence in the Brazilian parliament does exhibit anomalous diffusion [1]. And it seems that Lithuanian Seimas does too [2].

Data

We have accessed the open data available from Lithuanian Seimas website on 2019-06-08. Based on the voting registration data we have reconstructed presence data for the 2008-2012 and 2012-2016 legislatures. We have assumed that if the representative has registered to voter on at least one issue in that days agenda, then the representative was present that day.

There was a minor issue with some representatives leaving Seimas (dying, being elected to another post and etc.) and thus their record being incomplete. While in such cases their replacement should be elected as soon as possible, not always the replacement managed to be elected before the next session. So, while we detected replacements and joined the presence record of the predecessor and successor, there still was some data missing. In such cases (around 10%) we have replaced such invalid records with copies of valid ones. This replacement procedure shouldn't have profound effect on the results.

We have made the cleaned up data set available on GitHub (find it here).

Observing anomalous diffusion

Let us encode presence of representative \( i \) in \( t \)-th daily session as:

\begin{equation} \eta^{(i)}_t = 1 . \end{equation}

Likewise let us encode absence as:

\begin{equation} \eta^{(i)}_t = 0 . \end{equation}

Now let us study the cumulative presence data during selected legislature:

\begin{equation} x^{(i)}_{t+1} = x^{(i)}_{t} + \eta^{(i)}_{t+1} . \end{equation}

As in previous posts on anomalous diffusion we will consider mean and standard deviation of \( x^{(i)}_t \) series. Note that in this case our ensemble will consist of \( 141 \) trajectories, each corresponding to a representative in Lithuanian Seimas.

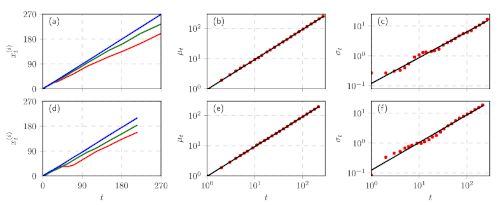Fig. 1:(figure from my paper) Empirical presence time series of selected representatives ((a) and (d)), also mean ((b) and (e)) and standard deviation ((c) and (f)) series for the considered legislatures. While mean grows linearly, standard deviation exhibits sub-linear growth with power law exponent equal to 0.85.

Note that similar analysis was conducted using Brazilian parliamentary presence data in [1]. In the paper by Vieira and others anomalous diffusion, actually ballistic regime, was found. With the Lithuanian data we can confirm the presence of anomalous diffusion, yet we fail to confirm the presence of ballistic regime (the growth of standard deviation is sub-linear in our Lithuanian Seimas data set). This might be due to the difference in parliaments as well as in the different way we treat the missing data. Some insights to the systematic difference will be given in next post in which we will consider a voter model as model for the parliamentary presence.

Acknowledgment. This post was written while reviewing literature relevant to the planned activities in postdoctoral fellowship ''Physical modeling of order-book and opinion dynamics'' (09.3.3-LMT-K-712-02-0026) project. The fellowship is funded by the European Social Fund under the No 09.3.3-LMT-K-712 ''Development of Competences of Scientists, other Researchers and Students through Practical Research Activities'' measure.

References

• D. S. Vieira, J. M. E. Riveros, M. Jauregui, R. S. Mendes. Anomalous diffusion behavior in parliamentary presence. Physical Review E 99: 042141 (2019). doi: 10.1103/PhysRevE.99.042141.
• A. Kononovicius. Noisy voter model for the anomalous diffusion of parliamentary presence. Journal of Statistical Mechanics 2020: 063405 (2020). doi: 10.1088/1742-5468/ab8c39. arXiv:2001.01479 [physics.soc-ph].