Cellular network

The term "cellular network" might confuse some readers as it also bears a meaning of the mobile phone network. Yet this time we will not talk about the mobile phone networks, though it is quite possible to say a lot about them from a point of view of the network theory and the most recent research. This time we will consider a new, at least on Physics of Risk website, network topology and at the same time network formation model.

Note 2024: The model we are referring here as "cellular network" in the modern literature is more commonly referred to as the "stochastic block model". "Cellular network" term was borrowed from course I have been watching at the time of writing this post.

Interestingly enough this network topology is very intuitive, yet formal definition it was given only recently. One of the first works to formally define cellular networks was published 8 years ago (see [1]). One should probably start to familiarize himself with cellular networks from that paper, but we will share some brief and less formal information on the same topic.

Comment added in 2024: It has recently come to my attention that this network formation model is also known under the name of "stochastic block model". It was introduced back in [2].

Cellular network - what is it?

Cellular network is a network, topology of which has well pronounced groups of nodes (in a similar manner as we have seen core and periphery in the core-periphery networks), which are connected with distinct topology. The distinctness of the topology might be minor - larger density of the edges between the nodes might be enough. Look at Fig. 1 below. The separate group of nodes are so well pronounced that it appears that they were grown separately and only then joined to form the network.

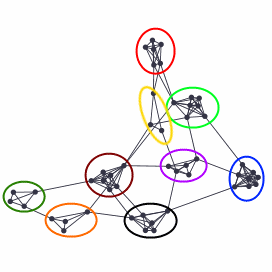Fig. 1:Example of a cellular network. In this figure we see 9 marked (using distinct colors) 'cells' of nodes.

Why are the cellular networks intuitive? Imagine that people live on the island (example taken from [3]). Moving by land is not very hard, so it is natural to expect that most islanders will know each other. While moving by water is a harder task, so the communication with inhabitants of other islands will be extremely rare. So, what topology does the social network have? Cellular network! Actually you need no exotic assumptions about the islands, because most of the people form most of their relationships in the place they spend most time in - educational institutions (schools, universities, ...), workplaces or leisure places.

How to make a cellular network?

The answer was already given - you just need to grow distinct parts of the network separately and afterwards connect them. It is important for the connection mechanism to differ at least somewhat. For example, we could grow network parts by using Erdos-Renyi model and later connect them using Barabasi-Albert model. But let us more broadly discuss a simpler case.

So let us start with \( N \) nodes. Let's place each node, upon creation, in a random point of the finite 1-dimensional space. Now let us split the space into \( N_c \) even parts. These parts are actually our "growth" cells. Inside these cells let us use Erdos-Renyi model to connected the nodes with probability \( p_{ic} \). After iterating over all cells, let us now create connections between them using the same Erdos-Renyi model, but now the nodes in different cells will be connected with probability \( p_{bc} \) (which should be significantly smaller than \( p_{ic} \)). After completing this step we would obtain a cellular network model.

References

• T. L. Frantz, K. M. Carley. A Formal Characterization of Cellular Networks. Center for Computational Analysis of Social and Organizational Systems, 2005.
• P. W. Holland, K. B. Laskey, S. Leinhardt. Stochastic blockmodels: First steps. Social Networks 5: 109-137 (1983). doi: 10.1016/0378-8733(83)90021-7.
• M. O. Jackson, B. W. Rogers. The economics of small worlds. Journal of the European Economic Association 3: 617-627 (2005). doi: 10.1162/jeea.2005.3.2-3.617.