Core-periphery network models

Do you remember a talk "Who controls the world? " given by J. B. Glatterfelder on the ted.com website? If not, you could go ant watch now or rely on us. As far as we remember the key point behind the talk is a scientific discovery of a fact that few hundred of large financial institutions control majority of the smaller financial institutions all around the world. Interestingly enough these large financial institutions also control each other! In this text we will give some examples which will show that similar network topology may form not only due to the conspiracy of these institutions, but also due to the other reasons.

Thus in this text we continue our topic on the network formation models. This time we will be interested in the so-called core-periphery network formation models, which will grow networks with well pronounced core and periphery.

Core and periphery in the networks

From time to time, even then using Erdos-Renyi or Barabasi-Albert network formation models, we may obtain networks with two differently wired groups of nodes. Lets say that the first group of nodes is tightly interconnected, while the other is very sparsely interconnected or not interconnected at all. Though the nodes in the second group are connected to the nodes from the first group. In this case the first group would be called a core, while the second would be referred to as a periphery. The concepts of the network core and periphery are visually explained in Fig. 1.

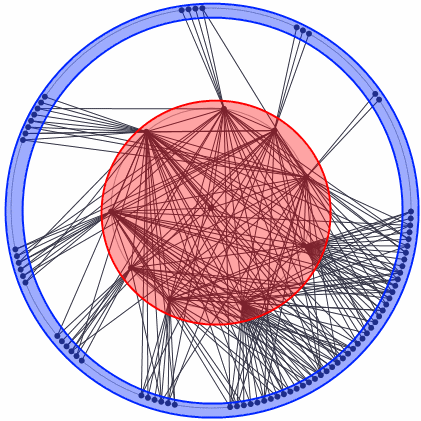Fig. 1:Core-periphery network generated using the modified Erdos-Renyi model. Nodes in the red area belong to core, while the nodes in the blue area are in periphery.

What is so special about the core-periphery networks? They are very resilient in a sense that ideal core-periphery network does not suffer much from the removal of nodes. Namely if you remove a node from an ideal core-periphery network, it doesn't matter if you remove core or periphery node, you do not destroy the network structure. If you remove the core node, the other core nodes will still have the same links the removed node had, so no other nodes would get separated from the surviving network. If you remove a periphery node, you just remove an unimportant node, which was just connected to the core and not to other nodes, so once again you have just remove a single node and a couple of edges. So, no matter which node you remove, the surviving network remains interconnected. It is worthwhile to note that real core-periphery networks are far from being ideal, yet the impact of node removal would still be comparatively small - only one branch of networks nodes would be separated from the surviving network and its size would be significantly smaller than the size of the whole network.

Obtaining ideal core-periphery network

It is not very hard task to generate the ideal core-periphery network. At first you should decided how many nodes will make up the core of the network. Next create the selected number of nodes and connect them (all nodes to all nodes!). Then add a chosen number of periphery nodes. Connect them to all of the core nodes. In this manner you will obtain an ideal core-periphery network.

Fig. 2:Ideal core-periphery network.

Yet this network topology is pretty boring - it is deterministic (only influenced by an externally made choice)! What else should we expect.

This algorithm, and some simple, but less ideal, are describe in the paper by Borgatti and Everett [1] (see it if you want to know more).

"Destroy the core-periphery network" challenge!

We have written above that the core-periphery networks are almost indestructible. Namely they are immune to node removal. You can test this claim using the app below. Your aim should be a destruction of the network without fully destroying its core. The nodes are destroyed by pressing "X" button, which is found near every node. If it is necessary you can move the nodes by dragging, and also restart app by pressing ">" button.

Modifying Erdos-Renyi model to recover core-periphery network model

We could randomly "grow" a core-periphery network by using Erdos-Renyi model. To make task easier let us modify the Erdos-Renyi model. First let us assume that our nodes are of two types and thus the connection probabilities become inhomogeneous. Namely we now will have not one, but multiple connection, edge forming, probabilities depending on which two nodes could be connected. As three distinct parings are possible we will have three distinct connection probabilities: \( p_{11} \) for the two nodes of first type to be connected, \( p_{22} \) for the two nodes of second type to connected and finally \( p_{12} =p_{21} \) for the connection between the nodes of differing types.

To completely avoid determinism we will assign types to nodes randomly - we will have a probability \( p_{c1} \) that a new node is of the first type, and \( p_{c2} \) that a new node is of the second type. To avoid some problems, or possibly overly complex implementation of the model, we will assume that the first type nodes are the core nodes and we will require that at least one node of this type actually exists.

Note that the app shows only the nodes which are connected to the core nodes. All of the other nodes are not shown.

Similar algorithm is used in [2, 3]. Reference [2] considers a network model based on the deterministic utility functions (with conditional payoffs depending on the agent types), while the network considered in reference [3] is random, but its connection probabilities are inter-coupled.

The core and periphery formed in this case due to the assumption we put in the model. Namely we decided to have two types of nodes - attractive ones (core nodes) and less-attractive ones (periphery nodes).

Core-periphery networks form the Barabasi-Albert model

We can also obtain a network with almost scale-free structure, visible core and periphery. This time the modification of the underlying model is rather minimal - we just have to assume that the "growth" of the scale-free network starts from \( N_{0} \) fully interconnected nodes and further the original algorithm is used. Note that in this case we will observe newly formed hubs (the nodes with large degrees) in the periphery, though the core nodes should still have larger degrees.

This time the core was dictated by the history of the network - it existed before we started to grow the network.

Strategic emergence of the core-periphery network topology

We have already written that [2] work relies on the utility functions to shape the core-periphery network. But how is it possible? For a start let us note that the utility functions of each agent (which is placed in the network nodes) depends on the network topology. Namely if an agent can easily communicate with many other agents, his utility function is larger. It appears that such agents should form completely connected network. The intuition is right, but in the real world in order to keep relationship (or connection) alive the nodes have to pay a certain price. So the completely connected network is no longer effective nor desired by the agents. They now attempt to gain as much from communication with other agents, but to lose as few resources as possible. In certain cases, for details see [2], in this interplay of cost and benefit the core-periphery network topology emerges.

So the core-periphery network topology may also emerge from a need to cooperate. Direct communication is costly, so part of the agents have to play a role of hubs. It is worth to recall that in the model proposed in [2] the agents are divided into core and periphery agents, so the core forms not for the natural endogenous reasons, but once again it forms from the exogenous reasons. This may be bypassed by assuming that agents initializing connection have to pay whole "price" for the connection (namely to have directed network). In such case the hubs are being subsidized by the periphery and thus may emerge endogenously [4].

References

• S. P. Borgatti, M. G. Everett. Models of core/periphery structures. Social Networks 21: 375-395 (2000). doi: 10.1016/S0378-8733(99)00019-2.
• D. Persitz. Power and Core-Periphery Networks. SSRN, 2010: 1579634. doi: 10.2139/ssrn.1579634.
• M. P. Rombach, M. A. Porter, J. H. Fowler, P. J. Mucha. Core-Periphery Structure in Networks. CoRR abs/1202.2684: 1-27 (2012). arXiv: 1202.2684 [cs.SI].
• D. Hojman, A. Szeidl. The Payoff to Being Central: Core and Periphery in Networks. 2006.