Clifford attractor

Typically due to friction (or other dissipative forces) physical systems reach stationary states, even if it takes really long time. Nonlinear systems, on the other hand, sometimes exhibit strange and erratic behavior.

Clifford attractor

Clifford attractor is generated by iterating following set of iterative equations:

\begin{equation} x_{i+1} = \sin\left(f_1 y_i\right) + A_1 \cos\left(f_1 x_i\right) , \end{equation}

\begin{equation} y_{i+1} = \sin\left(f_2 x_i\right) + A_2 \cos\left(f_2 y_i\right) . \end{equation}

Where \( f_1 \), \( A_1 \), \( f_2 \) and \( A_2 \) are parameters, whose values determine the shape of the attractor (the figure you generate).

We have already explored another set of iterative equations, those were based on quadratic polynomials, few years back (see the old post). As this set of iterative equations are based on \( \sin \) and \( \cos \) functions, expect to see more of attractors have circular or spherical appearance.

Gallery

Here are few interesting shapes I was able to find either online or using the search function of the app below.

Fig. 1:Infinity

Fig. 2:Sphere inside the sphere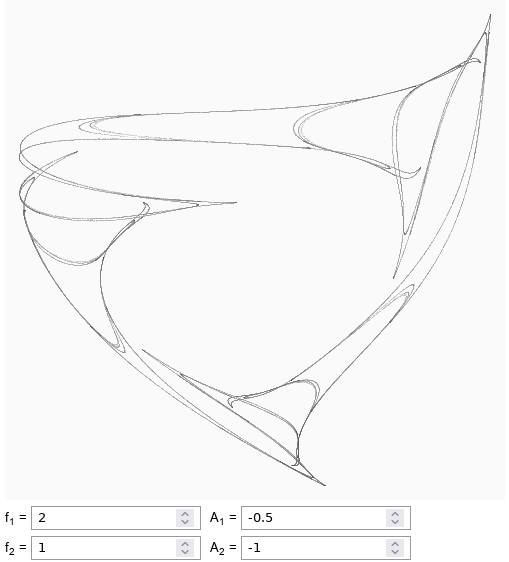

Fig. 3:Loopy triangle

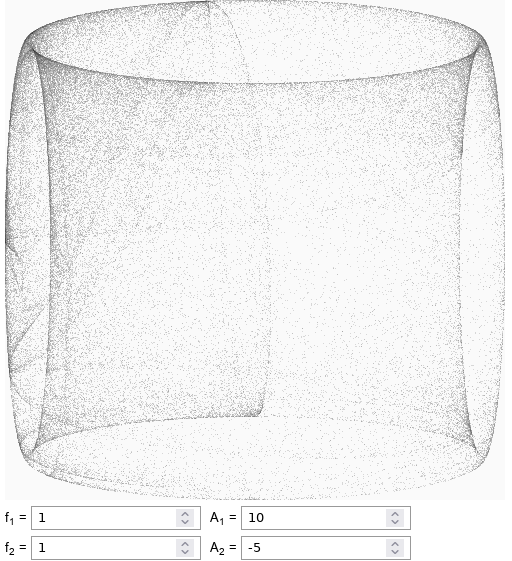Fig. 4:Six sided die

The shades of gray you are seeing in these figures correspond to the number of the attractor trajectories passing each pixel.

Interactive app

This interactive app will help you generate Clifford attractors. You can either select your own parameter values or generate them randomly (by pressing randomize).

Not all attractors you'll find will be interesting. If after a quick moment the plot goes red, this means that you have found a quite boring attractor. Under such circumstances the generation will be automatically stopped.

In some cases attractors will not occupy whole area of the plot, as the naive estimation of bounds will not always be correct. In this case you should press "Resize" button, which will select new plot limits based on the recently generated points. This should give more optimal limits.

If you are unlucky in your search for another nice random Clifford attractor, then you can automate the search by pressing "Search" button. In this case the app will try different random parameter values until an interesting attractor is found. To stop the search simply click either "Stop search" button or "Stop" button.

In my experience interesting Clifford attractors are easier to find than quadratic polynomial attractors we have looked at earlier. For Clifford attractors slight modifications of the parameter values should not completely destroy the shape of the attractor. So you can play with parameter values to perfect the shape you are looking at.