Randomly generated strange attractors

In classical physics differential equations is the main tool to mathematically describe dynamical systems. Having obtained the mathematical descriptions of the system we should be able to predict the evolution of the system. It is noted that the evolution of the classical systems is pretty trivial - no matter what the initial condition is the system will "find" the stable state. Usually dissipative forces (such as frictions) are to be blamed for this. Though not all systems are so simple...

In the literature those stable state are frequently called attractors. These attractors can not only "pull in" trajectories, but they also can "repel" them. Furthermore on the two dimensional plane one other types of attractors might exist. For example certain attractor might "pull in" some trajectories and at the same time "repel" some of them. Some attractors might even "force" the trajectories cycle around them. But the most interesting attractors are known as strange attractors and they "force" strange, supposedly random or chaotic, behavior around them. This behavior most of time posses features of dynamical chaos and has fractal features (ex., fractional dimension).

We will further consider the generation of these, strange, attractors...

Method

The essence of this method is a solution of the non-linear recurrence equations. Generally speaking the set of equations might be composed of two or more iterative equations and the exponent of non-linearity might have very different values. In this text we will limit ourselves to the case of the two equations with quadratic non-linearity. Namely:

\begin{equation} \left\{ \begin{aligned} x_{n+1} =& a_0 x_n^2 + a_1 x_ny_n + a_2 x_n + a_3 y_n^2 + a_4 y_n + a_5 , \\ y_{n+1} =&b_0 x_n^2 + b_1 x_n y_n + b_2 x_n + b_3 y_n^2 + b_4 y_n +b_5 , \end{aligned} \right. \end{equation}

here \( a_i \) and \( b_i \) are random coefficients. Each of these coefficients is given a random value in \( [-2, 2] \). This random value is assigned at the start of every new evaluation of the series.

Note that not all of the randomly generated coefficient sets will make up attractors with interesting properties. Most of the time you will actually obtain the trivial cases of convergence, divergence of trajectories or cyclically orbiting trajectories. Consequently any piece of software used to generate the strange attractors in this manner should have some kind of "filter" implemented to drop the trivial trajectories.

Gallery of the random attractors

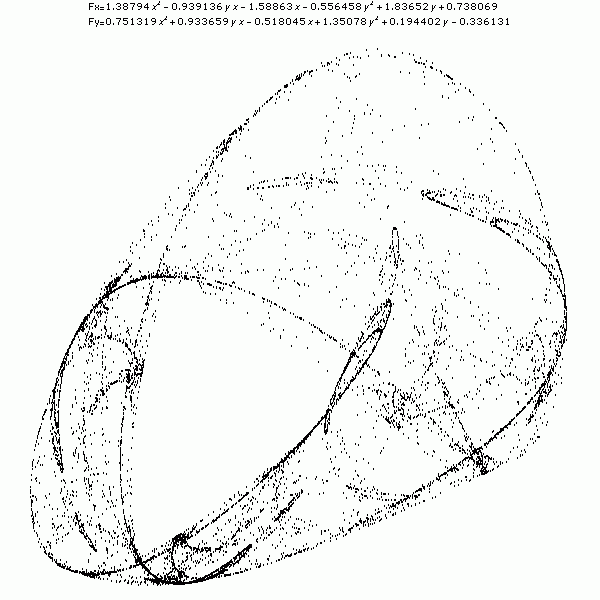Fig. 1:Stone

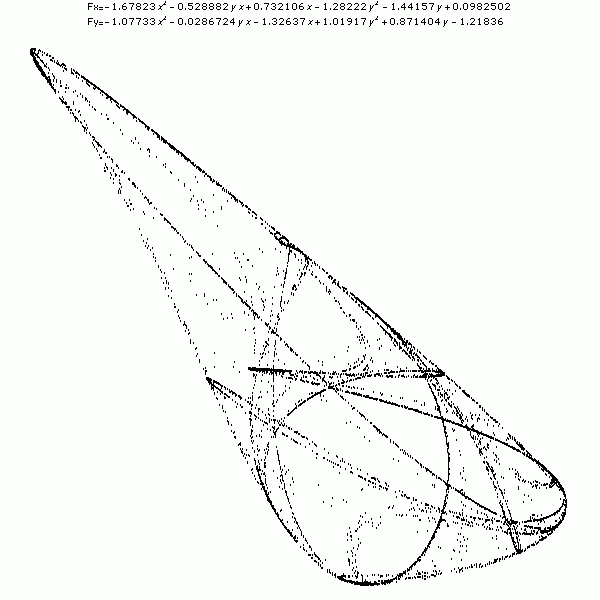Fig. 2:Spaceship

Fig. 3:Swan

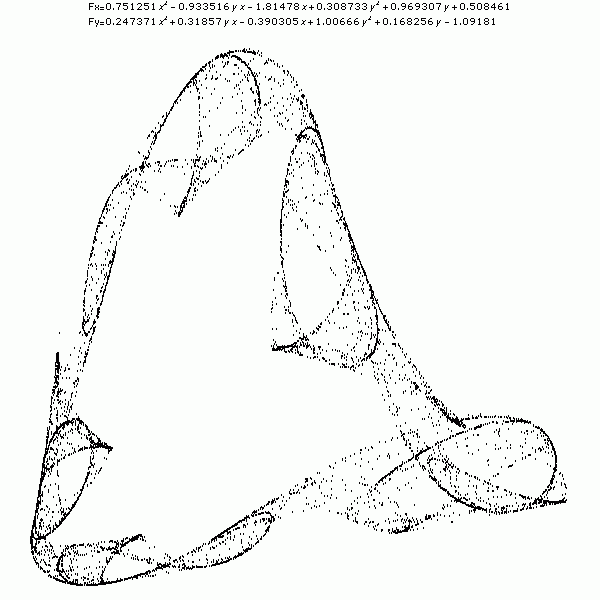Fig. 4:Mountain

Fig. 5:Bird

Fig. 6:Crocodile

Fig. 7:Cylinder

Fig. 8:Hourglass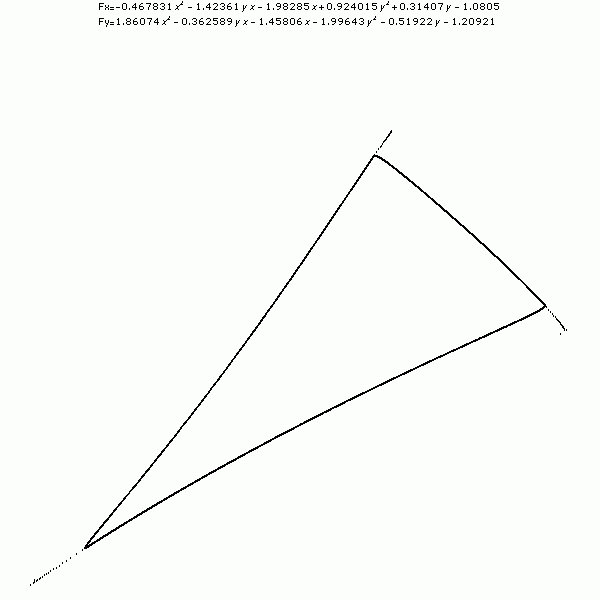

Fig. 9:Triangle

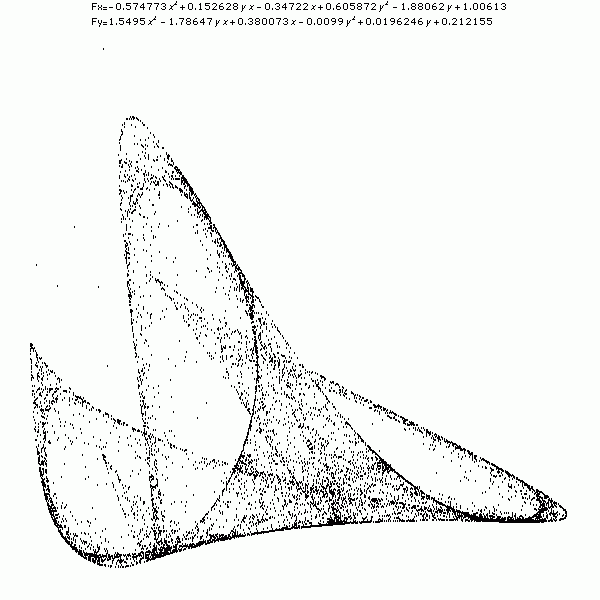Fig. 10:UFO

Interactive model

Below you should be able to fined small applet, which enables generation of random strange attractors (using the method discussed above). In this applet we have implemented some filters, which remove the trivial attractors, though note that the algorithm behind the filter is a very simple, thus it is probable that some of the trivial results will still appear. We encourage you to actively use the "Generate attractor" button.

The applet uses 5 shades of gray to color the trajectory points. The brighter point is the older it is (namely it was generated earlier than a darker one). Therefore in certain cases, if the stable cyclic trajectory exists and is reachable within 5000 iterations, black points will correspond to the trajectory of strange attractor.

Previously the interactive model was powered by Wolfram CDF technology. The old app can still be downloaded from here.