Lotka-Volterra equations
The simplest ecological system can be constructed from the two interacting species, e.g., prey and predator. This kind of system is very interesting in the terms of Physics of Risk primarily because it is nonlinear [1], and due to being real life example of competition (conflict). Also there are few known simple models for the prey-predator interaction. Among them there are both macroscopic, Lotka-Volterra equations, and microscopic, agent-based, models. We will start our discussion from the macroscopic Lotka-Volterra model.
Lotka-Volterra equations
Instead of simply writing down the equations let us briefly discuss what is going on in this kind of system. Interestingly enough the ideas we will discuss are also applicable for the socio-economic modeling [2, 3, 4, 5, 6]. Yet we choose the ecosystem for the discussion as in this case all interactions should be pretty clear and straightforward.
First let us start with the natural birth-death processes. The numbers of both prey and predator are changing at certain rate. For the sake of simplicity we could assume that this rate is constant and depends only on the current number of individuals. Though it is worthwhile to note that there are some works considering non-constant and even stochastic rates. For the sake of simplicity we could also assume that the prey can only increase its abundance. This might be seen as an assumption that prey would live infinitely long if not getting eaten by the predator. Also we could assume that predator population should naturally decrease. The thought behind this is that predators need to be full and strong to be able to produce an offspring. Under these assumptions the birth-death terms might be expressed in the terms Malthus and Verhulst models:
\begin{equation} \mathrm{d} X = a X \mathrm{d} t \quad\text{or}\quad\mathrm{d} X = ( a X - b X^2 ) \mathrm{d} t . \end{equation}
Our interest lies in the non-linear terms, which stand for the interaction of the species. It should be evident that the population of prey should decrease due to inter-species interaction, while the predator population should grow. The probability of the meeting of the prey and the predator is proportional to the both sizes of the respective populations. Taking it into account we can finally write the Lotka-Volterra equations, in the general form:
\begin{equation} \mathrm{d} X_i = \left[ a_i X_i - b_i X_i^2 - \sum_{j\neq i} c_{ij} X_i X_j \right] \mathrm{d} t , \end{equation}
here i is an index related to the certain species, while c parameters describe the interaction between species labeled by index i and j. If c is positive, then i-th species is suffering from j-th, otherwise the species is gaining from the interaction.
Note that the general form of Lotka-Volterra equations can describe the interaction of more than two species, though this text is dedicated to the two species prey-predator interaction. If the populations can growth is not limited, then the set of Lotka-Volterra equations will look like this:
\begin{equation} \mathrm{d} X_1 = \left[ a_1 X_1 - c_{12} X_1 X_2\right] \mathrm{d} t , \quad \mathrm{d} X_2 = \left[ -a_2 X_2+ c_{21} X_2 X_1 \right] \mathrm{d} t , \end{equation}
here index 1 is used with variables related to the prey population, while index 2 marks the relation to the predator population. All parameters in these equations are positive numbers - the nature of interaction is already accounted for.
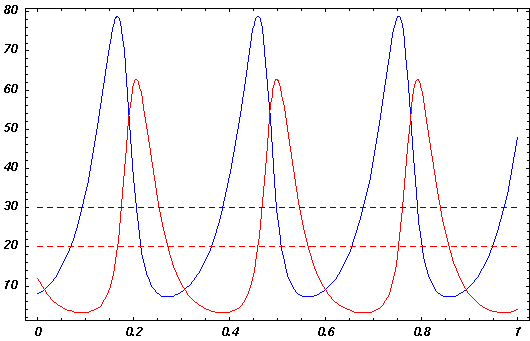 Fig. 1:Solution of the Lotka-Volterra equations. Red line marks the predator evolution, while blue - prey's. Dashed lines mark the model's fixed points. Parameters: \( X_1(0)=8 \), \( X_2(0)=12 \), \( a_1=20 \), \( a_2 =30\), \( c_{12}=c_{21}=1 \).
Fig. 1:Solution of the Lotka-Volterra equations. Red line marks the predator evolution, while blue - prey's. Dashed lines mark the model's fixed points. Parameters: \( X_1(0)=8 \), \( X_2(0)=12 \), \( a_1=20 \), \( a_2 =30\), \( c_{12}=c_{21}=1 \).In Fig 1. we have shown one of the possible solutions of the Lotka-Volterra equations. The example demonstrates essential qualitative behavior of the model - its "fluctuating" nature. These "fluctuations" are inherent to a real life system. If predators are few, then the prey population has an opportunity to grow as the predators are able to catch less prey than new prey are born. On the other hand if the prey population becomes abundant many predators will be satisfied enough to bear an offspring. The growing predator population will consume more of prey, until at certain the consumption will become larger than the reproduction of the prey. After this the population of prey will start to decline. The predator population will soon follow, because the decreased abundance of food will cause mass starvation. We will one again find our ecosystem in the state with few prey and few predators, so the prey population will once again grow... In this manner the history will repeat itself.
Repetition might be avoided if both populations arrive at the respective fixed point at the same time or the model starts with the initial conditions equal to the fixed points. Note that for the prey this fixed point is a ratio between the qualities of the predator population, \( a_2 / c_{21} \), while the predators depend on the qualities of the prey population, \( a_1 / c_{12} \). The better for prey, the better for predator, while the better for predator, the worse for prey. This is very interesting, though ultimately simple, example of conflict and cooperation in the actual real life system.
Interactive Lotka-Volterra model applet
Previously, instead of the currently used HTML5 app, we have used an app based on the Wolfram CDF technology. The old app is still available for download.
Stochastic Lotka-Volterra model
In the recent scientific literature [1, 5, 7, 8, 9, 10] one can find many examples of not only the deterministic, previously discussed, Lotka-Volterra model, but also of its stochastic treatment. Usually randomness is introduced into the model by making simple assumption about the random nature of the external forces acting on the species (e.g., random food supply for the prey) or the random nature of the internal forces obviously influencing the interaction of the populations.
In the first case, \( a_i \rightarrow \bar a_i + \sigma_{a,i}\mathcal{N}_i(0,1) \), one obtains linear (with the respect to the noise) set of stochastic differential equations:
\begin{equation} \mathrm{d} X_i = \left[ \bar a_i X_i - b_i X_i^2 -\sum_{j \neq i} c_{ij} X_i X_j \right] \mathrm{d} t +\sigma_{a,i} X_i \mathrm{d} W_i . \end{equation}
The non-linear (with the respect to the noise) stochastic differential equations can be obtained by both assuming the random capacity (external feature) of the species and by randomizing interaction parameters. Let us assume the latter, \( c_{ij} \rightarrow \bar c_{ij} -\sigma_{c,ij} \mathcal{N}_{ij}(0,1) \):
\begin{equation} \mathrm{d} X_i = \left[ a_i X_i - b_i X_i^2 - \sum_{j\neq i} \bar c_{ij} X_i X_j \right] \mathrm{d} t + \sum_{j\neq i} \sigma_{c,ij} X_i X_j \mathrm{d} W_{ij} . \end{equation}
In the above stochastic differential equation W, as common, stands for the Wiener process or standard Brownian motion. We won't further analyze the stochastic model, though we would like to draw the readers attention to the fact that this model can be applied to economics and financial markets. Furthermore the stochastic Lotka-Volterra model might be used to obtained the power law probability density functions observed in those complex systems [5, 9].
References
- N. S. Goel, S. C. Maitra, E. W. Montroll. On the Volterra and Other Nonlinear Models of Intereacting Populations. Reviews of Modern Physics 43: 231-276 (1971). doi: 10.1103/RevModPhys.43.231.
- M. Ausloos. On religion and language evolutions seen through mathematical and agent based models. Proceedings of the First Interdisciplinary Chess Interactions Conference, pp. 157-182. Canada, 2009. arXiv: 1103.5382 [physics.soc-ph].
- R. M. Goodwin. A Growth Cycle. In: Socialism, Capitalism and Economic Growth, ed. C.H. Feinstein. Cambridge University Press, 1967.
- N. L. Olivera, A. N. Proto, M. Ausloos. Information Society: Modeling A Complex System With Scarce Data. Proceedings of The V Meeting on Dynamics of Social and Economic Systems 6: 443-460 (2011). arXiv: 1201.1547 [physics.soc-ph].
- S. Solomon. Generalized Lotka Volterra (GLV) Models of Stock Markets. In: Applications of Simulation to Social Sciences, ed. G. Ballot, G. Weisbuch, pp. 301-322. Hermes Science Publications, 2000. arXiv: cond-mat/9901250.
- N. K. Vitanov, M. Ausloos, G. Rotundo. Discrete model of ideological struggle accounting for migration. Advances in Complex Systems 15 (supp01), 2012: 1250049. doi: 10.1142/S021952591250049X.
- M. Arato. A Famous Nonlinear Stochastic Equation (Lotka-Volterra Model with Diffusion). Mathematical and Computer Modelling 38: 709-726 (2003). doi: 10.1016/S0895-7177(03)90056-2.
- X. Mao, S. Sabanis, E. Renshaw. Asymptotic behaviour of the stochastic Lotka-Volterra model. Journal of Mathematical Analysis and Applications 287: 141-156 (2003). doi: 10.1016/S0022-247X(03)00539-0.
- S. Solomon, P. Richmond. Stability of Pareto-Zipf Law in Non-stationary Economies. In: Economics with Heterogeneous Interacting Agents, Lecture Notes in Economics and Mathematical Systems, 503: 141-159. Springer, 2001. arXiv: cond-mat/0012479 [cond-mat.stat-mech].
- C. Zhu, G. Yin. On competitive Lotka-Volterra model in random environments. Journal of Mathematical Analysis and Applications 357: 154-170 (2009). doi: 10.1016/j.jmaa.2009.03.066.
