Newton-Raphson method
Newton-Raphson, sometimes just Newton or Newton-Fourier, method is an approximate method in mathematical analysis for finding local roots of very complex functions (such as polynomials with large powers). Recall that root of the function is defined as a solution of \( f(z) = 0 \). The essence of this method is to linearize function at the guessing point. The point where linearized function passes the abscissa axis is assumed to be a more precise estimate of the actual root. Mathematically:
\begin{equation} z_{n+1} = z_n - \frac{f(z_n)}{f'(z_n)}, \end{equation}
here \( z_n \) is our previous guess (also the point of linearization). The n-th guess of the root is assumed to be precise enough if \( | z_{n} - z_{n-1} | < \varepsilon \) (here \( \varepsilon \) is allowable error). Note that if n-th guess matches root precisely (t.y. \( f(z_\infty)=0 \)) error equals zero, \( |z_{n} - z_{n-1} | = 0 \).
Simple example
Let us solve \( x^2 + 2 x +1 = 0 \) (\( f(x)=x^2+2 x+1 \), \( f'(x)=2 x+ 2 \), \( \frac{f(x)}{f'(x)} =\frac{1+x}{2} \)):
| Iteration | n-th root | f(z)/f'(z) | n+1-th root | Error |
|---|---|---|---|---|
| 1 | -2 | -0.5 | -1.5 | 0.5 |
| 2 | -1.5 | -0.25 | -1.25 | 0.25 |
| 3 | -1.25 | -0.125 | -1.125 | 0.125 |
| 4 | -1.125 | -0.0625 | -1.0625 | 0.0625 |
| 5 | -1.06258 | -0.03125 | -1.03125 | 0.03125 |
Here we can stop by assuming that our allowable error \( \varepsilon = 0.04 \).
Application towards complex numbers
As we know polynomial with n-th power has n roots. The problem is that not all of them can be real valued! In such case one will have to search complex number plane. If one is willing to find more than one root one should make more than guess. These two requirements can be solved rather simply. One just should take some region of the complex plane and skim through it at some fixed step. Each step corresponds to making new guess from the associated, smaller, region. By coloring these regions according to the success of the guess on would obtain map. These maps tend to have fractal structure and thus are known as Newton-Raphson fractals.
In the image below you see solution of \( z^2+2 \imath z+1=0 \) one the complex plane (real and imaginary parts are constrained in [-5;5]).

While this image is not breathtaking, it is perfect for understanding of the method - in it you can clearly see how different guesses converge towards roots. Brighter regions mean that root is found faster, while different colors belong to the different final roots.
Complex cases and root basins
Let see how method fares in case of more complex equation - \( z^5+z^3+2 \imath z+1=0 \). Let the real part of expected roots be constrained in [0;5], while imaginary being in [-0.25;1.75]. In the image below we can see three different roots. Though only one is seen fully, while the others are seen only partly (via basins).
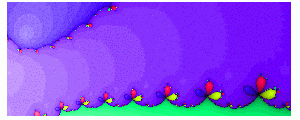
But what happens near the edge of basin?

As we can see interesting thing happen on the edge - many small basins are attached to the larger one. Attachment should persist at different scales meaning that even smaller basins are attached to the smaller basins. Interestingly enough neither of basins has root inside them (thus "jumps" to the other places on the complex plain occur in the eyes of each basin).

Let's analyze one more complex case - \( z^7+15 z^4+3=0 \). Let real and imaginary part of roots be constrained in [-5;5]. This we can clearly see six different roots, while seventh is hardly seen as it is the only real root and convergence towards it is very slow.

Below you can see the case then two different basins "interact" with each other.
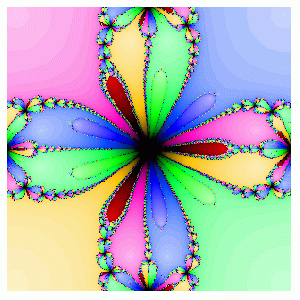
In the image below you can see small root basins overlapping. Note that even smaller root basins are overlapping. These overlaps would persist at any scale.

Newton-Raphson fractal generator
We have called this fractal generator NeRFEx (abbrevation from Newton Raphson Fractal Explorer). Note that Java applet has some functions disabled, those functions are made available in standalone java program (you can download its English or Lithuanian localization).
To start working with fractal generator press "Open NeRFEx in new window". Pop-up shall open and you'll be see main GUI of NeRFEx.
