The Saint Petersburg paradox

In the 1738, Daniel Bernoulli, the very same known for his contribution to fluid dynamics, in his paper in the "Commentaries of the Imperial Academy of Science of Saint Petersburg" described an interesting paradox. Let us assume that we have a fair 50-50 game in which the host tosses a coin until the tail appears. After each toss he pays a player \( 2^n \) (where \( n \) is a number of the toss) of money. The problem in question is - what is an optimal price for the game? Namely how much money the host should ask from a player, that he would be still motivated to play the game, yet also preventing unnecessary losses by the host.

There is no direct answer for this problem, because the expected winnings are infinite,

\begin{equation} \mathbf{E} = 2 \cdot \frac{1}{2} + 4 \cdot \frac{1}{4} +\ldots + 2^n \cdot 2^{-n} + \ldots = \sum_{i=1}^\infty 2^i\cdot 2^{-i} = \infty , \end{equation}

while the player does not believe that he would be able to win that much.

What is wrong? The problem in question requires the game to posses the characteristic scale, while there is no characteristic scale in this problem.

I have seen this paradox for a first time in a book by Mantegna and Stanley [1], yet slightly earlier I have seen an inverse formulation of the paradox. In the inverse formulation the lack of characteristic scale is seen more clearly (and dangerously).

Inverse formulation

Once during the under-graduate years one friend have told me that he invented a "fool-proof" gambling strategy. The strategy assumes a fair, or almost fair, 50-50 game and suggests the player to bid 1 unit of money after each win, while the bid should be doubled after each loss (2 units after first loss, 4 units after the second, ..., \( 2^n \) after the n-th). The strategy appears to be "fool-proof" as the cumulative loss grows as \( 2^n -1 \), thus after the streak of losses has been broken (and it will eventually be broken) the player still makes a profit.

But what if he losses more than he has money? No real person has an infinite amount of money required by this "fool-proof" strategy. So in the end some streak of losses will be a final streak as the player will be unable to further increase his bets.

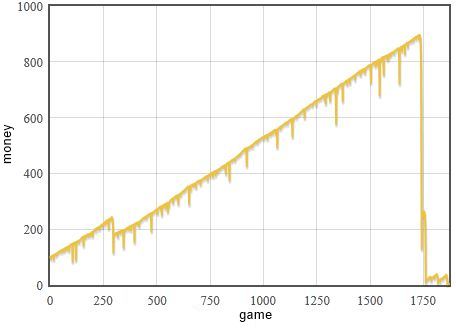Fig. 1:One of the tipical realizations while using the discussed strategy. As everything goes well it appears that there is no risk - income is steady, but even shortest streak of losses might result in a bankruptcy.

Browser applet

References

• R. N. Mantegna, H. E. Stanley. Introduction to Econophysics: Correlations and Complexity in Finance. Cambridge University Press, 2000.