Multi-success heterogeneous detrapping process

When presenting heterogeneous detrapping process at the DPG conference I got a question (or a suggestion to check) what would happen if instead of heterogeneous traps we would require multiple successes for the charge carrier to escape? In the previous post we have seen that this change makes relatively little difference when the detrapping times are exponential. But what if they are power-law? What if we require \( N_{success} \) successes within the heterogeneous detrapping process?

Sum of power-law distributed random values

When summing power-law distributed random values, the resulting distribution maintains a power-law tail, with the index of this tail remaining approximately consistent with the original values being summed. Intuitively, this occurs because in the aggregation of multiple values, the largest value often dominates significantly over the others, thereby influencing the overall sum disproportionately. So, overall, nothing should change?

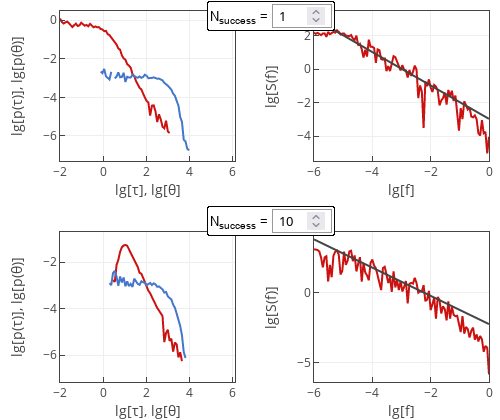Fig. 1:Sample simulation results with different required number of successes.

When running the simulation, we see one somewhat important difference: for larger \( N_{success} \) the higher frequency cutoff (critical frequency at which the spectral density transitions into Brownian motion regime) moves to the left. In other words, the range of frequencies for which 1/f noise is observed shrinks. Also, the small detrapping times become exceedingly rare - a sharp cutoff is introduced into the detrapping time distribution.

Interactive app

Now we invite you to play around with \( N_{success} \) parameter value and check what happens.