Verhulst correction to Doomsday model

In a previous post we have taken a look at a model, which predicts doomsday to fall on November 13, 2026 [1]. The prediction was made based on the best fit to the data available in 1960. Recent available data deviates from the prediction made in [1]. Instead it seems to be more consistent with Verhulst model.

Here in this post we modify the doomsday model by introducing correction, inspired by Verhulst's improvement upon Malthus model, to the driving ordinary differential equation.

Corrected Doomsday model

The original ODE is given by [1]:

\begin{equation} \frac{d N}{d t} = \alpha N^{1/k+1} . \end{equation}

This singularity can be removed by multiplying right hand side by an additional term, which would go to zero as \( N \) approaches some critical population \( M \) (its value can be interpreted as maximum supported population). Let that term be: \( 1 - \left( \frac{N}{M} \right)^\mu \). Then the ODE:

\begin{equation} \frac{d N}{d t} = \alpha N^{1/k+1} \cdot \left[ 1 - \left( \frac{N}{M} \right)^\mu \right] . \end{equation}

All that is left is to find proper values for the parameters. As far as my quick exploration shows, multiple choices are viable. Feel free to find your own. One that I found is shown in the figure below.

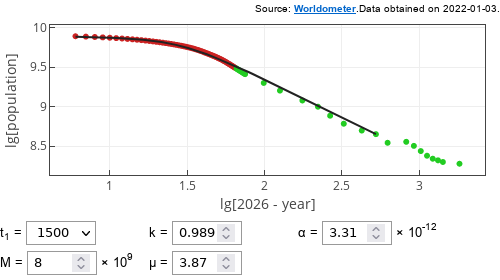Fig. 1:One of the reasonably looking fits of the corrected Doomsday model to the world population data.

Interactive app

This app is mostly identical to the one from the previous post. Though in this app \( t_0 \), doomsday date, parameter is no longer available (instead you can tune \( \alpha \) value). To keep visualization consistent with the results of original paper [1] we plot the data and model results as if 2026 was still a special year.

Note that the default parameters of the app are different from the best fit I have found. It is as it is to encourage you to find your own good looking fits.

References

• H. von Foerster, P. M. Mora, L. W. Amiot. Doomsday: Friday, 13 November, A.D. 2026. Science 132: 1291-1295 (1960).