Bornholdt's heterogeneous agent-based spin model for financial markets

Previously we have discussed ant colony model [1, 2] (see Kirman's agent based and stochastic model of ant colony), which is an interesting example of applying knowledge obtained from one field to another. Human (ex., trader in the financial markets) crowd behavior is ideologically quite similar to the behavior in ant colonies, thus the success and relevancy of the aforementioned model were to be expected. Though the key to success lies in the description of large number of entities.

Interestingly enough one can also create, and thus provide additional backing for the argument above, a successful model for human crowd behavior using classical models of statistical physics as an inspiration. In this text we will discuss agent-based spin model of the financial markets proposed by Bornholdt [3, 4], which is based on widely known Ising model. Despite the fact that Ising model models inanimate system, natural interactions are introduced by assuming two different types of interactions between the agents - local herding (local feromagnetic interaction) and global minority game (coupling with total magnetic field generated by whole lattice).

Bornholdt's model is also interesting as recently there were some attempts to propose macro treatment of the original agent-based model [5]. Previously similar thing was done with Kirman's model [2].

Bornholdt's modifications of Ising model

In the previous text on Ising model we have already mentioned that Ising model can be applied towards human crowd behavior modeling. One just have to imagine that each particle within the grid is agent representing some subject in the modeled system (ex., human). In such case the spin of particle can be interpreted as agent's decision or opinion towards some question. As in the financial markets agents choose to buy or to sell stock - we can use simplest case (with spins point either up or down) of Ising model when applying it towards the financial markets.

The above analogy is very general, while Ising model has a lot of variations and interpretations, thus technical details about the actual models might differ by a lot. One of the most essential technical details is how agents make their decisions. In the Bornholdt's model agents are polled asynchronously using heat bath formalism. Meaning that randomly chosen particles are allowed to achieve thermal equilibrium while being in contact with a heat bath, whose temperature \( T\sim \frac{1}{\beta} \). Particle state, or alternatively agent decision, after polling statistically (Boltzmann distribution is used) depends on the energy of the state:

\begin{equation} p_{S_i(t+1) = 1} = \frac{1}{1+\exp(-2 \beta h_i(t))}\,,\quad p_{S_i(t+1) = -1} = 1-p_{S_i(t+1) = 1}\,, \end{equation}

here \( h_i(t) \) is local magnetic field acting on particle i. Note that the above probabilities were simplified by using the fact that possible \( S_i(t+1) \) values are restricted to +1 and -1, and that \( Z = \exp[-\beta h_i(t) S_i(t+1)]+\exp[\beta h_i(t) S_i(t+1)] \). Due to the first simplification it might appear that probabilities do not depend on the energy, the product of \( h_i(t) \) and \( S_i(t) \), while it should be noted that formally dependence persists.

Note that the time tick in the probabilities above is not the time tick used in applets figures. 6400 of spin flips (time ticks in the probabilities above) correspond to the single time tick in applet figures. Number 6400 is selected due to the number of agents in the grid (80x80).

In the simplest case of Ising model local magnetic field is created by the neighboring particles and the external magnetic field. In Bornholdt's model interaction with the neighboring particles is retained, but there is no external magnetic field. Instead particles interact with global magnetic field, which is created by all particles inside the grid. Thus in Bornholdt's model local magnetic field is be expressed as:

\begin{equation} h_i(t) = \sum\limits_{j=1}^N J_{ij} S_j(t) - \alpha C_i(t) \frac{1}{N} \sum\limits_{j=1}^N S_j(t) , \end{equation}

here \( N \) is a number of particles in the grid, \( J_{ij} \) - strength of local interaction between two particles (\( J_{ij} = 1 \) if particles i and j are neighbors, o otherwise constant equals zero), \( \alpha \) - strength of global interaction, \( C_i(t) \) defines if global interaction is antiferromagnetic, \( C_i(t) = 1 \), or ferromagnetic, \( C_i(t) = -1 \). These modifications and heterogeneity of agents, \( C_i(t) \), are required in order to introduce two mechanics - minority game and herding instinct - very common in agent-based model of the financial markets [6]. Transition of \( C_i(t) \) are defined according:

\begin{equation} C_i(t+1) = -C_i(t) , \quad \text{if} \quad \alpha C_i(t)S_i(t) \frac{1}{N} \sum\limits_{j=1}^N S_j(t) < 0 . \end{equation}

Briefly (for detailed explanation see [3]) the above scenario can be summarized as: agents in minority might panic and start to imitate majority (due to herding instinct), while agents in majority might see a possibility of making profit if they would join minority (one might draw analogy with the minority game). Thus one can simplify the expression of local magnetic field to

\begin{equation} h_i(t) = \sum\limits_{j=1}^N J_{ij} S_j(t) - \alpha\left| M(t) \right|, \end{equation}

here \( M(t) \) is average particle magnetization. In [4] it is assumed that this scenario describes behavior of chartist traders - those who optimistically or pessimistically follow global trends. While there is also a third kind of agents who are placed outside the grid.

Fundamentalists are assumed to be those agents outside the grid. They tend to become more active then the difference between fundamental value (which can be seen as "true" value) and actual price (which can be seen as "perceived" value) becomes large. As they expect that market will stabilize - price will move towards fundamental value. Thus fundamentalists sell if the price is larger than fundamental value (stock is overrated) and buy if the price is smaller (stock is underrated). Therefore they limit chartists' speculations and disallow large enormous deviations of price from the fundamental value (which can be seen as speculative bubbles).

Introducing price and volume

If there are \( m \) fundamentalists in the market and their influence equals \( a \), then this group creates excess demand, which equals:

\begin{equation} ED_f (t)= a m \ln \frac{P_f(t)}{P(t)} . \end{equation}

Evidently chartist excess demands is dependent on magnetization of the grid:

\begin{equation} ED_c (t) = b N M(t) , \end{equation}

here \( b \) is chartist influence on the market.

By assuming that trades occur through the market maker, who sets correct prices by balancing demands (original Walras scenario), one can obtain

\begin{equation} ED_f (t) + ED_c (t) = a m \ln \frac{P_f(t)}{P(t)} + b NM(t) = 0. \end{equation}

From the above expression one can defined log-price of the stock:

\begin{equation} \ln P(t) = \ln P_f(t) + \frac{b N}{a m} M(t) . \end{equation}

And in such case return:

\begin{equation} r(t, \Delta t) = \ln P(t) - \ln P(t-\Delta t) = \sigma\sqrt{\Delta t} \xi(t) + \frac{b N}{a m} \left[M(t) - M(t-\Delta t) \right] , \end{equation}

here \( \sigma \) is variability of fundamental value and \( \xi(t) \) is Gaussian random variable (unit variance, zero mean). If \( \sigma \) is small, then one will observe typical statistical properties of return - power law distribution of returns and clustering of volatility. Otherwise dynamics of the market will be overwhelmed by the changes of fundamental value - market will act according to the efficient market hypothesis (one will observe Gaussian distribution and White noise spectral density).

Under the assumption of market maker clearing the market one can also obtain expression of market volume. Note that if grid is not magnetized then price equals fundamental price, thus fundamentalists do not generate any demand. Though chartists also generate no excess demand in such case, yet both chartist groups generate their demands (as they are equal excess demand remains equal to zero). From Walras scenario follows that if magnetization is non-zero fundamentalists are forced by the market maker to make deals with the chartists, who were unable to make trades with other chartists. Therefore total amount of trade equals number of chartists in the majority group - some of them make trades with minority chartists, some trade with fundamentalists. By putting the above words into math one can express volume [4],

\begin{equation} v(t) = \frac{V(t)}{N} = b \frac{1 + \left| M(t) \right|}{2}. \end{equation}

Model results

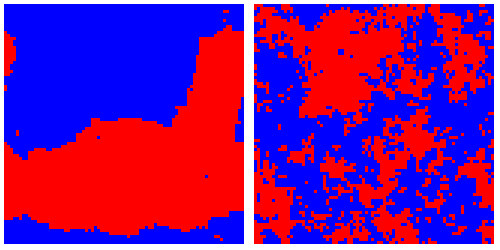Fig. 1:Phases observed in Bornholdt model: calmness (left figure), chaotic frustration (right figure). Note that Bornholdt model doesn't reach stable state - shown phases interchange during whole model evolution.

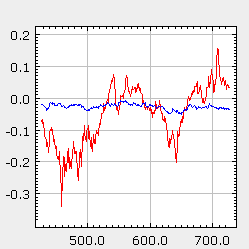Fig. 2:Evolution of log-price (red curve) and fundamental log-price (blue curve). Note that price fluctuations are by far stronger than fluctuations of fundamental price. Financial bubbles occur and end without major change in fundamental price.

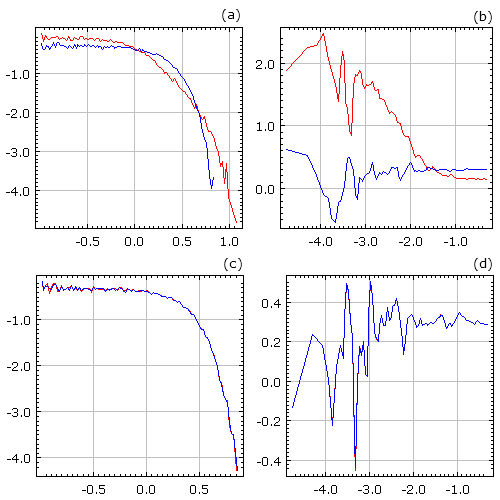Fig. 3:Statistical properties, probability density function ((a) and (c)) and spectral density ((b) and (d)), of normalized return (red curve) and changes of fundamental price (blue curve) observed in Bornholdt model. Figures (a) and (b) were obtained with small σ values, while (c) and (d) were obtained with significantly larger σ values. All figures use lg-lg scales. Note the (lack of) differences between statistical properties of return and changes of fundamental price.

HTML5 applet

The applet below models financial market using Bornholdt model, which was discussed above. Thus meaning of the parameters should be evident from previous discussion.

References

• A. P. Kirman. Ants, rationality and recruitment. Quarterly Journal of Economics 108: 137-156 (1993).
• S. Alfarano, T. Lux, F. Wagner. Estimation of Agent-Based Models: The Case of an Asymmetric Herding Model. Computational Economics 26: 19-49 (2005).
• S. Bornholdt. Expectation bubbles in a spin model of markets: Intermittency from frustration across scales. International Journal of Modern Physics C 12: 667-674 (2001).
• T. Kaizoji, S. Bornholdt, Y. Fujiwara. Dynamics of price and trading volume in a spin model of stock markets with heterogeneous agents. Physica A 316: 441-452 (2002).
• S. M. Krause, S. Bornholdt. Spin models as microfoundation of macroscopic financial market models. 2011. arXiv: 1103.5345 [q-fin.PR].
• M. Cristelli, L. Pietronero, A. Zaccaria. Critical Overview of Agent-Based Models for Economics. Proceedings of the School of Physics 'E. Fermi', Course CLXXVI, ed. F. Mallnace, H. E. Stanley, pp. 235-282. SIF-IOS, Bologna-Amsterdam, 2012. doi: 10.3254/978-1-61499-071-0-235.