Facebook contest data set exploration

During summer hiatus I have promised to look into a data set I have extracted from one particular Facebook contest. While many Facebook contests are not based on any logical reasoning, this contest appeals to me as it appears to require at least some thought or expertise. As far as I am aware, in Lithuanian schools, sets of linear equations are typical 8th grader problem. Even this low threshold allows to reasonably expect to observe herding behavior in the answers, because the ones who lack expertise will simply copy what the others have publicly written.

This contest is particularly interesting to me, because either intentionally or unintentionally there are infinitely many correct answers. It is so as the problem in the contest involves less equations (two) than unknowns (three). Hence there are no reasonable arguments for why to prefer one answer over the others.

The problem given for the contest

The organizers gave two linear equations,

\begin{equation} x + y = 3 , \end{equation}

\begin{equation} y + z + y = 3 . \end{equation}

The participants had to tell how much is \( z + x + x \). I leave the equations as they were shown in the original Facebook post.

Obviously the correct answer would be an expression, e.g., \( 9 - 4 y \), but the contest asked for a number, so the participants gave numbers as answers. There were couple angry comments about the incompleteness of problem, but they were significantly out numbered.

Structure of the data file

I have downloaded the comment data using Facebook's Graph API. Next I have classified the comments based on their content into 13 categories. Most of the comments belong to 1 of 10 categories ("ans0", "ans1", "ans2", "ans3", "ans4", "ans5", "ans6", "ans7", "ans8" and "ans9"), as people have guessed all 10 digits as possible answers. Interestingly enough no sincere guesses involved other numbers (neither two digits nor floating point numbers), though there were some "trolling" comments suggesting these comparatively ridiculously complex answers. These "trolling" comments were put in the same category ("corr") as the correct explanations that there many possible answers. There were also a couple of comments, which suggested that answer is either 3 or 5 ("ans35"), as well as a couple of comments providing reasoning why 5 is the only possible answer ("ans5a").

The other columns in the data file either store time in seconds since midnight 2018-07-09 ("time") or provide total number of comments giving some answers ("comments") at that time. Note that "time" column gives a time when comment was posted.

Feel free to download the data file (CSV).

Exploration

There 558 events in the data set, among them 553 gave some answer to contest, while 5 (less than 1%) tried to directly or indirectly (via unreasonable guesses) show that the contest provides ill-formed problem.

Out of the 553 guesses 92.5% (512) have guessed number 5. Why? Try to think of two number, which would sum to 3? At least I immediately think of 2 and 1. From this guess it is straightforward to arrive at to answer 5. Hence there were two comments suggesting that either of these can be answer. Notably there were five comments explaining why 5 is the only possible answer and no comments providing arguments for the other guesses.

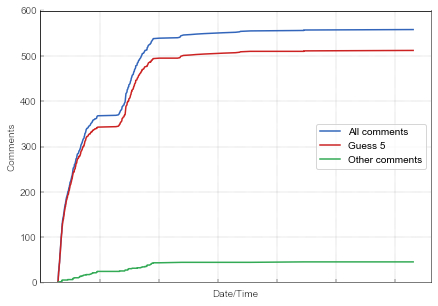Fig. 1:The growth of the number of comments. Blue line gives the total number of comments, red line indicates the total number of comments which have guessed 5, while the green line summarizes the total number of all other comments.

In Fig. 1 one can observe an interesting pattern: the curve seems to saturate twice. This observation is simply, because most of the people sleep at night. The first saturation occurs at midnight of the first day (vertical gridlines correspond to the midnights). The diffusion resumes the next day until the true saturation is reached over the next few days.

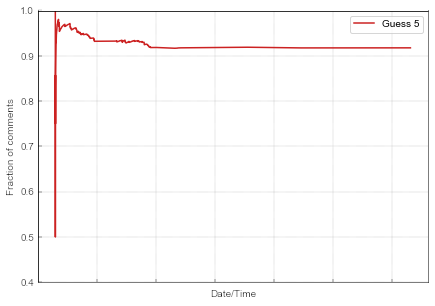Fig. 2:The evolution of the share of the Guess 5 comments.

Graph for the fraction of comments, Fig. 2, looks less interesting after some initial fluctuations (most likely due to finite size effects) the fraction of "Guess 5" comments quickly saturates at around 0.92.

Next time

In the next few posts I will address time-space (sigmoidal growth with multiple plateaus) and event-space ("Guess 5" comments being significantly more common) patterns we have observed here.