Long-range memory in nonlinear GARCH model

March 31, 2015 Aleksejus Kononovicius #interactive #economics #financial markets #stochastic models #A. Kononovicius #1/f noise #J. Ruseckas #ARCH process

Recently journal Physica A accepted our, A. Kononovicius and J. Ruseckas, manuscript titled "Nonlinear GARCH model and 1/f noise" [1]. In this article we shown that simple memory-less model with nonlinear term may exhibit interesting stylized fact - long-range memory. Our manuscript is even more interesting due to the fact that considered model (and its various modifications) is somewhat widely used by the practitioners.

Last time we have shown that GARCH(1,1) modeli is able to produce power law distributions, but not a long-range memory. In this text we introduce nonlinearity into GARCH(1,1) model and demonstrate that the modified model exhibits long-range memory.

Comparison between stochastic differential equation obtained from GARCH(1,1) and a general class of stochastic differential equations proposed by us and our colleagues [2, 3, 4],

\begin{equation} \mathrm{d} x = \sigma^2 \left( \eta - \frac{\lambda}{2}\right) x^{2 \eta -1} \mathrm{d} t + \sigma x^\eta \mathrm{d} W, \label{xsde} \end{equation}

shows that equations themselves are rather similar, but the similarity is restricted to \( \eta=1 \) case. Yet in order to reproduce long-range memory (1/f noise we need to have \( \eta\neq 1 \). This can be done by making some terms nonlinear. Let us write the following nonlinear process:

\begin{equation} \sigma^2_{t} = a_1 + b_1 \sigma^\mu_{t-1}\omega^\mu_{t-1} + c_1 \sigma^2_{t-1} , \end{equation}

here \( \mu > 2 \) is odd integer. This iterative equation may be rewritten as stochastic differential equation in respect to \( y= \sigma^2 \):

\begin{equation} \mathrm{d} y = \left( \frac{A}{y^{\mu-1}} -\frac{C}{y^{\mu-2}} \right) y^{\mu -1} \mathrm{d} t + | B |y^{\mu/2} \mathrm{d} W , \end{equation}

here \( A = \lim\limits_{h \rightarrow 0}\frac{a_{1,h}}{h} \), \( C = \lim\limits_{h \rightarrow 0}\frac{1-c_{1,h}}{h} \) and \( B^2 = \lim\limits_{h\rightarrow 0} \frac{b^2_{1,h} \langle \omega^{2 \mu}\rangle}{h} \) (note that index \( h \) means that parameters were obtained especially for the time scale in which \( h \) is a unit of time (in general case parameters in GARCH models depend on the selected time scale)).

The obtained equation is still a separate case of Eq. \eqref{xsde}, but now it is restricted by \( \lambda = 2\eta \). Having in mind that the comparison yields \( 2 \eta =\mu \), we may expect to control the slope of spectral density by changing \( \mu \):

\begin{equation} S(f) \sim \frac{1}{f^\beta} , \quad \beta = 1 +\frac{\lambda - 3}{2 \eta - 2} = 1 + \frac{\mu - 3}{\mu - 2} . \end{equation}

As you can see in a figure below, it does work rather well.

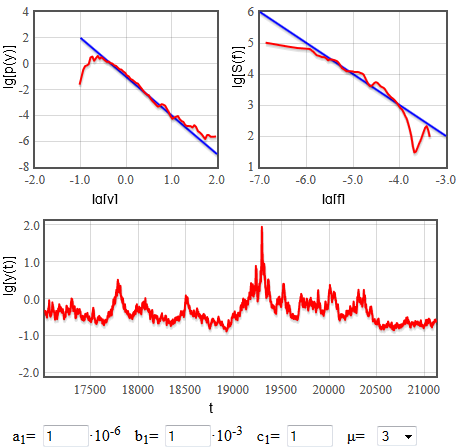Fig. 1:Reproducing 1/f spectra using nonlinear GARCH(1,1) model.

The comparison does not explain the roles of \( A \) (and thus \( a_1 \)) and \( C \) (and thus \( c_1 \)). Both these parameters determine the exponential cut-offs of the power law distribution. Namely stationary distribution of \( y \) has the following form:

\begin{equation} p(y) \sim \frac{1}{y^\mu} \exp\left[ - \frac{2A}{(\mu-1) B^2} \left( \frac{1}{y} \right)^{\mu-1} + \frac{2C}{(\mu-2) B^2} \left(\frac{1}{y}\right)^{\mu-2} \right] . \end{equation}

\( A \) determines where the exponential cutoff will occur, while \( C \) sets its shape. If \( C \neq 0 \), then exponential "bump" becomes more prominent, while power law tail event becomes less probable. Indeed, if you are interested in power law distribution and long-range memory, you should stick with \( C \) of the similar magnitude as \( \pm b^2 \). Thus \( c_1 \) should also be near \( 1 \) with a possible deviation of similar magnitude as \( \pm b^2 \). If deviations are larger, then Gaussian like distribution or divergence of the model might be observed.

We invite you to try HTML5 app below.

References

A. Kononovicius, J. Ruseckas. Nonlinear GARCH model and 1/f noise. Physica A 427: 74-81 (2015). doi: 10.1016/j.physa.2015.02.040. arXiv: 1412.6244 [q-fin.ST].
B. Kaulakys, J. Ruseckas. Stochastic nonlinear differential equation generating 1/f noise. Physical Review E 70: 020101 (2004). doi: 10.1103/PhysRevE.70.020101.
B. Kaulakys, J. Ruseckas, V. Gontis, M. Alaburda. Nonlinear stochastic models of 1/f noise and power-law distributions. Physica A 365: 217-221 (2006).
B. Kaulakys, M. Alaburda. Modeling scaled processes and \\\( 1/f^\beta \\\) noise using non-linear stochastic differential equations. Journal of Statistical Mechanics, 2009: P02051. arXiv: 1003.1155 [nlin.AO].