Power-law distribution in linear GARCH model

March 17, 2015 Aleksejus Kononovicius #Interactive models #economics #Stochastic models #financial markets #A. Kononovicius #J. Ruseckas #arch

Recently journal Physica A accepted our, A. Kononovicius and J. Ruseckas, manuscript titled "Nonlinear GARCH model and 1/f noise" [1]. In this article we shown that simple memory-less model with nonlinear term may exhibit interesting stylized fact - long-range memory. Our manuscript is even more interesting due to the fact that considered model (and its various modifications) is somewhat widely used by the practitioners.

In the next couple of blog posts we will present the main results of the manuscript. We will start with a simple demonstration that GARCH(1,1) model may exhibit power law distributions

The main idea behind GARCH models is very simple - some economic variables are heteroskedastic. Namely they may be modeled as two processes - one stochastic noise (most frequently Gaussian noise, though other noises are also used depending on the application), \( \omega_t \), while the other is deterministic standard deviation, \( \sigma_t \):

\begin{equation} z_t = \sigma_t \omega_t . \end{equation}

Standard deviation at time \( t \) depends on the past history of standard deviations as well as observables:

\begin{equation} \sigma^2_t = a + \sum_{i=1}^p b_i \sigma^2_{t-i}\omega^2_{t-i} + \sum_{i=1}^q c_i \sigma^2_{t-i} .\label{garch11} \end{equation}

If \( p > 1 \) or \( q > 1 \), then the system state is influenced not only by the current state, but also by its prior evolution. Thus such process does "remember" its own past. Yet if \( p=q=1 \), then the systems should remember only its current state and thus be memory-less.

Note that in case of \( p=q=1 \), equation for standard deviation looks very much alike difference equation. Thus \eqref{garch11} may be rewritten as a continuous process of \( y =\sigma_t^2 \):

\begin{equation} \mathrm{d} y = B^2 \left( 1 - \frac{\lambda}{2} +\frac{1}{2} \cdot \frac{y_{min}}{y} \right) y \mathrm{d} t + | B |y \mathrm{d} W , \end{equation}

here \( \lambda = 2 + \frac{1-b_1-c_1}{b_1^2} \), \( y_{min}=\frac{a_1}{b_1^2} \), \( B^2 \propto b_1^2 \). This stochastic differential equation is very similar to geometric Brownian motion, thus its spectral density should be Browninan-like, \( S(f)\sim 1/f^2 \).

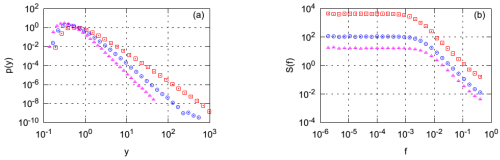Fig 1.Stationary probability density function of y (a) and spectral density of its time series (b). The following parameters were used: \( a_1=0.015 \), \( b_1=0.1 \), \( c_1=0.89 \) (red squares), \( 0.88 \) (blue circles), \( 0.87 \) (magenta triangles).

This is confirmed by our numerous papers [2, 3, 4], in which we consider a general class of stochastic differential equations:

\begin{equation} \mathrm{d} x = \sigma^2 \left( \eta - \frac{\lambda}{2}\right) x^{2 \eta -1} \mathrm{d} t + \sigma x^\eta \mathrm{d} W. \end{equation}

We invite you to confirm that yourselves using HTML5 app below. Please allow the simulation takes its time - correct results appear when power law distribution becomes visible.

Next time we will be back with GARCH(1,1) - we will introduce nonlinear term into it and thus obtain a model exhibiting a long-range memory property.

References

A. Kononovicius, J. Ruseckas. Nonlinear GARCH model and 1/f noise. Physica A 427: 74-81 (2015). doi: 10.1016/j.physa.2015.02.040. arXiv: 1412.6244 [q-fin.ST].
B. Kaulakys, J. Ruseckas. Stochastic nonlinear differential equation generating 1/f noise. Physical Review E 70: 020101 (2004). doi: 10.1103/PhysRevE.70.020101.
B. Kaulakys, J. Ruseckas, V. Gontis, M. Alaburda. Nonlinear stochastic models of 1/f noise and power-law distributions. Physica A 365: 217-221 (2006).
B. Kaulakys, M. Alaburda. Modeling scaled processes and \\\( 1/f^\beta \\\) noise using non-linear stochastic differential equations. Journal of Statistical Mechanics, 2009: P02051. arXiv: 1003.1155 [nlin.AO].