Nonlinear feedback and long-range memory in GARCH model

Recently journal Physica A accepted our, A. Kononovicius and J. Ruseckas, manuscript titled "Nonlinear GARCH model and 1/f noise" [1]. In this article we shown that simple memory-less model with nonlinear term may exhibit interesting stylized fact - long-range memory. Our manuscript is even more interesting due to the fact that considered model (and its various modifications) is somewhat widely used by the practitioners.

In previous blog posts we have demonstrated that one can reproduce power law distributions using GARCH(1,1) model and also that nonlinear GARCH(1,1) model enables reproduction of long-range memory. In this blog post we once again touch the topic of long-range memory, but now we consider nonlinear feedback.

Previously we have written down iterative equation, which has rather inconvenient restriction - nonlinearity exponent \( \mu \) may be only odd integer. This requirement was set as \( \omega \) may be both positive and negative, thus some times it may be problematic to raise it to certain power. This problem is solved by writing down the following equation with respect to \( \sigma^2 \):

\begin{equation} \sigma_t^2 = a_1 + b_1 \sigma_{t-1}^\mu |\omega_{t-1} |^\mu + \sigma_{t-1}^2 - c_1 \sigma_{t-1}^\mu .\label{ngarch112} \end{equation}

Now \( \mu \) may be any real number. Yet having in mind a general class of stochastic differential equations proposed by our colleagues [2, 3, 4],

\begin{equation} \mathrm{d} x = \sigma^2 \left( \eta - \frac{\lambda}{2}\right) x^{2 \eta -1} \mathrm{d} t + \sigma x^\eta \mathrm{d} W, \label{xsde} \end{equation}

we restrict ourselves to \( \eta > 1 \) or, alternatively, \( \mu > 2 \). HTML5 applet below is further restricted to integer values, but this was done just for the sake numerical efficiency.

Eq. \eqref{ngarch112} may be rewritten in continuous time as stochastic differential equation with respect to \( y=\sigma^2 \):

\begin{equation} \mathrm{d} y = \left( \frac{A}{y^{\mu-1}} +\frac{C}{y^{-1+\mu/2}} \right) y^{\mu-1} \mathrm{d} t + |B|y^{\mu/2} \mathrm{d} W_t . \end{equation}

This equation is essentially identical to Eq. \eqref{xsde} and to stochastic differential equation obtained in previous blog post. Comparing to the equation from the previous blog post the only apparent difference is the power of \( y \) in term with \( C \) parameter. Less apparent is the difference in relation between the parameters. In this case they are as follows: \( A =\lim\limits_{h \rightarrow 0} \frac{a_{1,h}}{h} \), \( C =\lim\limits_{h \rightarrow 0} \frac{b_{1,h} \bar{\omega}_\mu-c_{1,h}}{h} \) and \( B^2 = \lim\limits_{h \rightarrow 0}\frac{b^2_{1,h} \hat{\omega}_\mu}{h} \) (here \( h \) indexes once again represent time scale sampled using \( h \) time steps (in general case parameter values in GARCH model may depend on the selected time scale); \( \bar{\omega}_\mu = \langle | \omega |^\mu\rangle \), \( \hat{\omega}_\mu = \langle [ |\omega|^\mu -\bar{\omega}_\mu ]^2\rangle \)). Thus we expect to see that:

\begin{equation} p(y) \sim y^{-\mu} , \quad S(f) \sim f^{-1-\frac{\mu-3}{\mu-2}} . \end{equation}

Fig. 1 confirms this as we are able to reproduce 1/f noise.

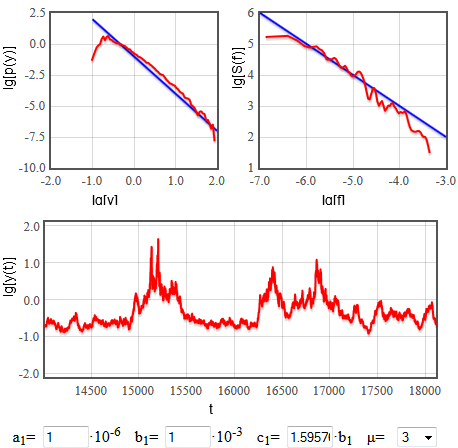Fig. 1:Reproducing 1/f noise using nonlinear GARCH(1,1) model.

\( A \) and \( C \) once again affect the exponential cut-offs - \( A \) influences the placement of cut-off, while \( C \) describes how "prominent" is the exponential cut-off. Once again, if \( C \neq 0 \), interesting power law behavior is destroyed, thus we have to require that \( c_1 \approx b_1\bar{\omega}_\mu \). Note that in the HTML5 app below \( c_1 \) value is set in respect to \( b_1 \).

We invite you to try interactive HTML5 applet below.

References

• A. Kononovicius, J. Ruseckas. Nonlinear GARCH model and 1/f noise. Physica A 427: 74-81 (2015). doi: 10.1016/j.physa.2015.02.040. arXiv: 1412.6244 [q-fin.ST].
• B. Kaulakys, J. Ruseckas. Stochastic nonlinear differential equation generating 1/f noise. Physical Review E 70: 020101 (2004). doi: 10.1103/PhysRevE.70.020101.
• B. Kaulakys, J. Ruseckas, V. Gontis, M. Alaburda. Nonlinear stochastic models of 1/f noise and power-law distributions. Physica A 365: 217-221 (2006).
• B. Kaulakys, M. Alaburda. Modeling scaled processes and \\\( 1/f^\beta \\\) noise using non-linear stochastic differential equations. Journal of Statistical Mechanics, 2009: P02051. arXiv: 1003.1155 [nlin.AO].