q-Voter model with non-conformers

One of the differences between how social scientists and sociophysicists view the modeling of social systems is the outlook towards independent behavior. Importance of individuality underlies many theories in social sciences, while physicists are used to explain various emergent properties through interactions. Obviously both approaches are oversimplifications of objective reality. This time we consider another generalization of the q-Voter model in which a group of physicists and social scientists attempted to bridge this gap.

Two years ago we have already explained that properties of individual agents in some cases do not matter, because they average out. This is obviously true if we build models from perspective of physics. But if we include intuitions from social sciences, then this "truth" might no longer be true. Thus in some cases minute details about individuality of agents can have interesting effects on the dynamics of the modeled social systems.

So here we discuss a generalization of the q-Voter model using so-called diamond model of social response [1]. An interesting result reported in [1] is that two different psycho-social approaches to non-conformative behavior generate somewhat different results when introduced into the q-Voter model.

The diamond model for social responses

The core idea of the diamond model is that there are four possible responses to an external influence [2]:

• Conformity. After being exposed to an opposite opinion, agent changes his opinion to conform.
• Independence. After being exposed to some opinion, agent ignores it and keeps his own.
• Anti-conformity. After being exposed to some opinion, agent changes his opinion to disagree with it.
• Variability. After being exposed to some opinion, agent changes his opinion regardless of the source.

Conformative behavior is already present in numerous sociophysical models. What is missing from the most of them is details about non-conformative behavior. Usually these details are hand-waived and simple noise is used to reflect non-conforming behavior in agents. Yet as we can see there are three types of non-conformist behaviors.

Building the diamon model into the q-Voter model

[1] builds two different models based on the q-Voter model. First one (A model) incorporates anti-conformist behavior, second one (I model) incorporates independence and variability (which are actually two sides of the same, random behavior, coin). In the article and its precursor articles (e.g., [3]) it is shown that these two models have different critical values.

Before discussing the critical values let us provide an algorithms for each model. A model:

1. Pick a random agent.
2. With probability \( p_a \) agent is anti-conformist. He will disagree with his \( q \)-panel. Otherwise agent is conformist and will agree with his \( q \)-panel (as usual in the q-Voter model).
3. Select \( q \) neighbors of the selected agent. If all neighbors have the same opinion, the selected agent changes his opinion to either agree (if he is conformist) or disagree (if he is anti-conformist) with the selected \( q \)-panel.

I model:

1. Pick a random agent.
2. With probability \( p_i \) agent is independent. His opinion will be flipped with probability \( 1/2 \). Otherwise agent is conformist and will agree with his \( q \)-panel (as usual in the q-Voter model).
3. If the agent is conformist, then select \( q \) neighbors of his. If all neighbors have the same opinion, the selected agent changes his opinion to agree with the selected \( q \)-panel.

Critical values, when the model is executed on the complete graph, are the following: for the A model \begin{equation} p^*_a=\frac{q -1}{2 q}, \end{equation} and for the I model \begin{equation} p^*_i=\frac{q -1}{q -1 + 2^{q-1}}. \end{equation}

If the probabilities are larger than the critical probabilities, then disordered (anti-ferromagnetic) phase should be observed in the dynamics of that model. Otherwise ordered (ferromagnetic) phase should be observed. Note that for \( q>5 \) I model has a rather complicated behavior in the vicinity of critical probability. Namely, both phases appear to coexist.

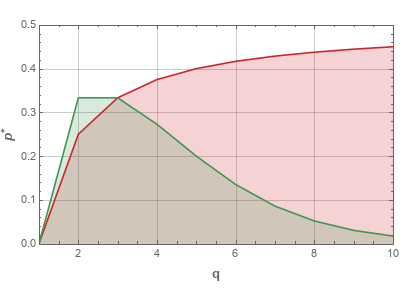Fig. 1:Phase diagram for the A model (red) and I model (green). Lines show the critical value dependence on q. Ordered phase area is shaded.

HTML 5 apps

Here we provide you a single app, which evaluates both models with the same non-conformity probability. Explore the difference in the dynamics of the models with larger values of \( q \) and intermediate probabilities. I model should be quick to enter disordered phase, while A model should enter this phase with a bit larger \( p_a \).

You can also study the models separately using separate app for each of the models. Click here to find the app for the A model and click here for the I model.

Acknowledgment. This post was written while reviewing literature relevant to the planned activities in postdoctoral fellowship ''Physical modeling of order-book and opinion dynamics'' (09.3.3-LMT-K-712-02-0026) project. The fellowship is funded by the European Social Fund under the No 09.3.3-LMT-K-712 ''Development of Competences of Scientists, other Researchers and Students through Practical Research Activities'' measure.

References

• P. R. Nail, K. Sznajd-Weron. The Diamond Model of Social Response within an Agent-Based Approach. Acta Physica Polonica A 129: 1050-1054 (2016). doi: 10.12693/APhysPolA.129.1050.
• H. R. Willis. Conformity, Independence and Anticonformity. Human Relations 18: 373 (1965). doi: 10.1177/001872676501800406.
• P. Nyczka, K. Sznajd-Weron, J. Cislo. Phase transitions in the q-voter model with two types of stochastic driving. Physical Review E 86: 011105 (2012). doi: 10.1103/PhysRevE.86.011105.