Spin glass model

Previously on Physics of Risk we have already discussed the Ising model, which is one of the most fundamental models in statistical physics. We are especially interested in Ising model as it is frequently applied to model social systems. One of such examples is the Bornholdt model of the financial markets.

This time we will consider a modification of Ising model, which describes disordered magnet (a so-called spin glass). In this text we will briefly cover the essential feature of spin glasses as well as provide interactive HTML5 applet of the spin glasses.

What is a disordered magnet?

Let us remind you that in normal magnets, magnetic moments of interacting particles align in one particular fashion. The interactions are either ferromagnetic (the spins align in the same direction) or anti-ferromagnetic (the spins align in the opposite directions). In disordered magnet we may have different types and strengths of interactions at the same time.

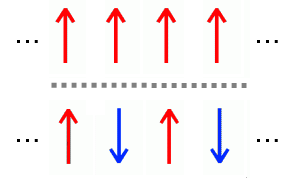Fig 1.Spin orientation in ferromagnetic and anti-ferromagnetic materials.

In low temperature, in absence of thermal noise, normal magnets reach ordered state. While disordered magnets quickly freeze in the disordered state.

The simplest spin glass model may be obtained by assuming that \( J \) of the original Ising model are normally distributed random variables. Note that set of \( J \) should be pregenerated prior to the modeling it self and should not be changed during the modeling.

HTML5 applet

In the applet below we present the implementation of the modified Ising model on 50×50 2D square lattice. In the applet window you can see four figures - current spatial spin distribution graph, evolution of energy, entropy and magnetization. Single iteration corresponds to the one thousand attempts to change the spin of the random particle. After every iteration each figure is renewed. Numerical calculations are started by pressing button "Start" and can be stopped by pressing button "Stop". After stopping the calculations user can resume them or restart them from the beginning.

This applet is a slightly modified version of previous applet, which was available on the original page about Ising model. Thus you can also see options relevant for the original Ising model - namely you can enable ferromagnetic ("J=1") interactions or anti-ferromagnetic ("J=-1") interactions. Note that critical temperature of the original Ising model in this applet was around \( \frac{\Delta E}{k T} = 0.4 \) (you may want to use this value with other "J=..." options).