Aleksejus Kononovicius: What can the Bass diffusion model tell us about piracy?

Recently in Lithuanian and world's different or global social spaces there was a lot of disccusion on anti-piracy and the proportionality of so-called "protection" of intelectual properties. The US politicians consider SOPA and PIPA, while EU countries one after another expressed will to join ACTA. In Lithuanian media and blogosphere, as most probably in the rest of the world, has split into the ACTA supporter and opposition camps.

It is rather easy to notice that representatives from both camps sometimes base themselves on the ideological "truths" and personal experiences. Most of arguments by the ACTA supporters nicely fit into the phrase "property is sacred", which is one of the main postulates of liberal ideology. The only thing that is strange here is that another postulate of the same ideology is the sacred nature of economic and social freedom of each individual. Which is obviously breached if very person using the Internet is assumed to be criminal by definition. ACTA's opposition relies on a more diverse set of arguments. Yet I find the notion of how common plagiarism and intellectual piracy is inside the intellectual creation process itself to be the key point. Actually I myself have dealt with artists who use pirated software to produce their intellectual product, yet asking money for their own service. In Lithuania we have also had numerous plagiarism scandals ranging from the music to monumental art (e.g., sculptures). But let us stop here while we can - we are interested in the fundamental truths, not ideology or personal experiences. Let us attempt to understand the actual and observed reality!

By the way on the Internet I have found two more-or-less professionally written texts (though I am aware that most probably there are more of them) - see lawyer M. Kiškis and sepuku.lt blogs. In the first text the ACTA is tackled from the legal point of view, while the second is based on the scientific research [1]. Further in text I will also rely on the scientific works relevant in terms of Physics of Risk - namely I will use the Bass diffusion model [2] and review by Prasad and Mahajan [3].

The links to other websites above are available only in Lithuanian. Writing this text I am mostly concerned with Lithuania, though the actual ideas below are not geo-centric. Either way for serious analysis in English I refer you to the cited works.

Introducing piracy into the Bass model

Evidently the piracy can be introduced into the Bass model by including "shadow" diffusion process, which unlike the main diffusion process does not provide profit, though otherwise it is the same. Thus the market potential is divided into the legal consumers and pirates. The ratio of between these groups is determined by the availability of the product (depends on the price and the consumers income) and the tolerance of piracy. Mathematically this ideas are put down like this [3]:

\begin{equation} \partial_t X(t) = f(p(t)) \left[ N-X(t)-Y(t) \right]\left[ \sigma +\frac{h}{N} \{X(t) - Y(t)\} \right] , \end{equation}

\begin{equation} \partial_t Y(t) = \alpha \left[ N-X(t)-Y(t) \right]\left[ \sigma +\frac{h}{N} \{X(t) - Y(t)\} \right] , \end{equation}

here \( N \) is a market potential (total amount of agents in the system, the theoretical limit for the product adoption), \( X \) - number of legal adopters at a given time, \( Y \) - number of pirates at a given time, \( \sigma \) - coefficient of innovation, \( h \) - coefficient of imitation, \( f(p(t)) \) - availability of product as a function of price, \( \alpha \) - tolerance of the piracy. The above equations might be further generalized by assuming that tolerance of piracy might vary in time and etc. Though for our simple analysis this model should suffice.

Model equations suggest that:

• If the price is large, and thus the availability of product is low, and/or piracy is tolerated, then piracy will prevail in the market. In the opposite case consumers will tend to choose legal product.
• Piracy hastens product diffusion.
• Piracy is the main cause for the lost profit.

First two suggestions are correct and are justified by analyzing empirical data. While the third suggestion is caused by the simplicity of the model - it is highly doubtful that all of the pirates would become legals under certain conditions. Another point ruling out the third suggestion is that precise evaluation of actual market potential is very troublesome task (if doable at all). Thus the profit might be also lost due to overestimation of the market potential.

The analysis of different scenarios: constant tolerance, initial tolerance and "charity"

Having in mind the aforementioned simplicity of the model let us study the curves plotted in Fig. 1. In this figure we see the diffusion of product if piracy is present (blue curve) and absent (green curve). Note that blue curve grows significantly faster than the green one, though the green one reaches larger value than the blue one. If piracy is present it "consumes" part of the market potential (red curve).

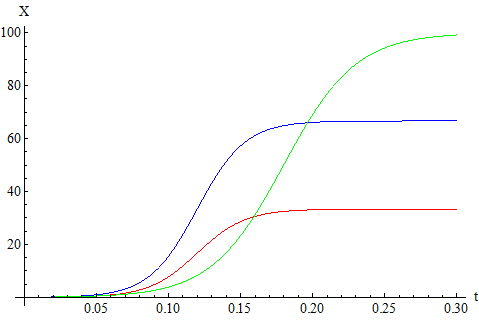Fig. 1:Bass diffusion without piracy (green curve) and with it (pirates - red curve; legal consumers - blue curve). Model parameters are identical in both cases. On the abscissa axis we plot time, t, while on the ordinate we plot the number of consumers, X.

One could stop tolerating piracy after a certain moment to gain both momentum and gain more money [3]. This scenario is shown in Fig. 2. Note that once again diffusion is faster then pirates are present, yet in this case larger profit is gained as more consumers are legals.

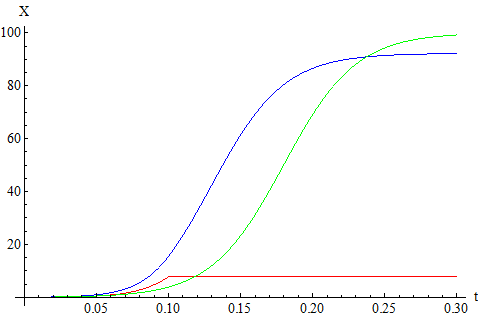Fig. 2:Bass diffusion without piracy (green curve) and with it (pirates - red curve; legal consumers - blue curve). Model parameters are identical in both cases.

One might consider another marketing strategy. One could further increase the speed of diffusion by giving away the product for free or with large discounts. The model stays the same as in case with "shadow" diffusion, but the "shadow" diffusion term remains constant, \( Y(t) = Y_0 \). As you can see in Fig. 3 profit loss once again stays minimal, yet the diffusion is even faster.

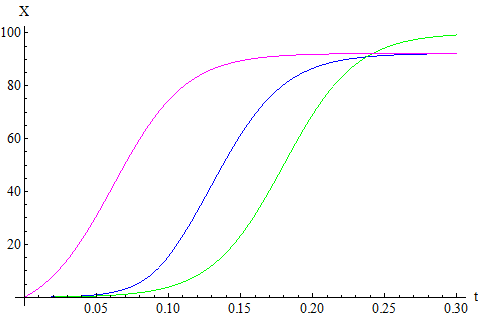Fig. 3:Bass diffusion without piracy (green curve), with pirates (blue curve) and in 'charity' scenario (magenta curve). Model parameters are otherwise identical.

The full effectiveness of the previous approach can not be seen from the point of our analysis. Recall that our model is very simple - namely modeled market doesn't have any structure (every agent is connected to every other agent), while the real markets have structures. Some elements of real markets have a lot more influence than others as they are socially active and widely available. Choosing to facilitate product diffusion among them would be a very wise choice as it would also significantly facilitate product diffusion among other market elements.

Somewhat ideological moral or "instead of conclusions"

As we have shown in the above tolerance of piracy is an excellent marketing tool, which helps to improve the spread of the newly introduced product. This conclusion also applies towards markets with competition (note that our simple model considers only monopolist market). It is so as if we would have two products of similar perceived quality and similar availability, market would adopt the one, which is more pirated, namely which tolerates the piracy more. This conclusion is also made in [3] after studying a bit more complex model.

Interesting, and important in context of ACTA, notion is that seeing piracy as excellent marketing strategy is not new. [3] argues that this strategy was used by Microsoft to obtain leading position in Taiwan market. And after obtaining leading position in Taiwan, Microsoft has cracked down software pirates in this country. Similar strategy was also used to conquer Chinese market, but the conquest is not yet completed thus the piracy in China is tolerated. This poses an interesting question - is the piracy genuinely a bad thing (as ACTA supporters claim) or it is just the market manipulation tool, which is not useful anymore in certain countries.

The "charity" scenario is also very interesting as it is even more effective than tolerance of piracy. So in order to gain the most we have to present the product to the most active social elements. In case of software there two very active social elements - governmental organizations and public (and private?) schools. Due to the software adoption in schools most of kids would assumed to be taught using only the presented software, thus after graduating they might be unable to use the other (possibly analogous) pieces of software. While software adoption in governmental organizations forces adults and business to adopt same kind of software, because effective electronic communication would be only possible if both parties use the same standardized software.

It is interesting to note, yet it is not surprising, that this strategy is also widely applied. In Lithuania most schools use the same software to teach kids. Thus in the end only a few school graduates are aware that Windows and Microsoft Office have their corresponding alternatives. Also most of governmental organizations use Microsoft Office "native" formats to convey information to the people (e.g., presenting templates .doc on their websites).

Therefore for me it is very strange why we have this situation? Why the (Lithuanian) politicians, who were not previously concerned with software piracy problems, without any discussion are eager to ratify questionable agreements, which possible infringe human rights? Why the first idea in their heads is to capture and punish? Why they do not care about educating society and increasing accessibility of electronic government (e.g., by legislating open standards)?

Note that this analysis is mostly based on the example of software piracy, yet the same mathematical formalism applies towards other types of industries. Though the other industries might have their own specific qualities, might be needed to account for on theoretical level. In case of multimedia industry one could use works by A. Ishii [4, 5, 6] to improve understanding of the diffusion of multimedia products. Though the specifics of the industries should not influence the general conclusions reached in this analysis.

You can explore these possibilities by using interactive applet available here.

References

• B. Dahaner, J. Waldfogel. Reel Piracy: The Effect of Online Film Piracy on International Box Office Sales. 2012. https://ssrn.com/abstract=1986299.
• F. M. Bass. A New Product Growth Model for Consumer Durables. Management Science 15: 215-227 (1969).
• A. Prasad, V. Mahajan. How many pirates should a software firm tolerate? An analysis of piracy protection on the diffusion of software. International Journal of Research in Marketing 20: 337-353 (2003).
• A. Ishii, S. Umemura, T. Hayashi, N. Matsuda, T. Nakagawa, H. Arakaki, N. Yoshida. Mathematical Model for Hit Phenomena. Proceedings of Econophysics Colloquium 2010. 2010. arXiv: 1002.4460 [physics.soc-ph].
• A. Ishii, H. Arakaki, N. Matsuda, S. Umemura, T. Urushidani, N. Yamagata, N. Yoshda. The hit phenomenon: a mathematical model of human dynamics interactions as a stochastic process. New Journal of Physics 14: 063018 (2012). doi: 10.1088/1367-2630/14/6/063018. arXiv: 1112.1143 [physics.soc-ph].
• A. Ishii, T. Matsumoto, S. Miki. Revenue Prediction of Local Event using Mathematical Model of Hit Phenomena. Progress of Theoretical Physics Supplements 194: 64-72 (2012). arXiv: 1112.0767 [physics.soc-ph].