401st post!

The post we have posted before the summer vacation was our 400th post! We haven't noticed this milestone at the time, but let us then celebrate 401st post by looking at the language statistics of our posts. Particularly, we can ask a question whether Zipf's law applies for our posts.

Technically this 402nd post, but it was written before the previous post. So let us still celebrate now :)

Zipf's law

Zipf's law is an empirical observation, that often in popularity (frequency, or size) tables the popularity decays as power-law function of rank:

\begin{equation} \text{popularity} \sim \frac{1}{\text{rank}^\alpha} . \end{equation}

With the dependence being close to the inverse law (i.e., \( \alpha \approx 1 \)).

So, will it hold?

Tag popularity

First we have checked whether Zipf's law holds for our tags. We have counted how many times each tag was used to tag a post. After the counting we have ranked (ordered) tags based on the respective popularity. To simplify the analysis, we have divided all counts by the top count (162 posts were tagged with Interactive models tag) thus obtaining their relative occurrences. Finally we have plotted the obtained data on log-log axes.

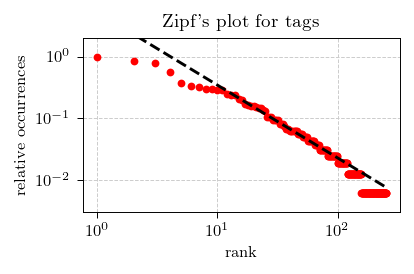Fig 1.Zipf's plot for the relative tag occurances on Physics of Risk website.

And you as can see in the figure above: red dots (the data) seems to be reasonably well approximated by the dashed line (a power-law function of rank). The exponent of the power-law function we have obtained is \( 1.18 \). Not perfect, yet reasonably close.

Word popularity

Next we have considered which words we use in our posts. This analysis is largely identical to what we have done with the tag popularity analysis, with one notable exception - we have used Porter Stemming Algorithm to reduce words to their stems. We have also done a lot of cleaning (such as removing meta information, equations, figures) on the raw data.

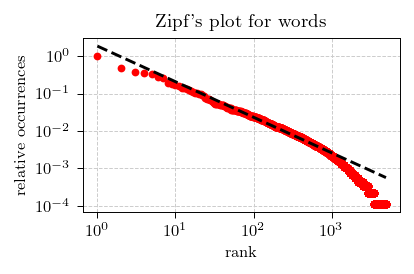Fig 2.Zipf's plot for the relative word occurances on Physics of Risk website.

Yet the picture we see (in the above) is remarkably similar: the data (red dots) reasonably well follows a power-law function of rank (dashed line). The exponent of the power-law function we have obtained is \( 0.95 \). Much closer to the expected unity.

As ought to be expected, the most popular words are articles ("a", "an", "the"), conjunctions ("and") and prepositions ("of", "in", "to" and others). Excluding these and some other boring words the most popular words were: "model" (ranked 8th), "agent" (21st), and "time" (24th). Which is somewhat expected as a lot of model discussed here on Physics of Risk are temporal agent-based models.