Elementary model reproducing q-Gaussian distribution

q-Gaussian distribution is rather interesting generalization of the well-known Gaussian distribution. This generalization arises from the generalized, non-extensive, statistical mechanics, which was proposed by C. Tsallis two decades ago. Despite the fact twenty years have passed there is no simple physical model reproducing the q-Gaussian distribution. But our colleague Julius Ruseckas recently proposed one [1]. In this text we will briefly discuss his "correlated spin" model and will present two related interactive applets.

In order to understand the main point behind the proposed model it is best to start from contrasting uncorrelated spin model. In this case each spin in our one dimensional lattice choose his orientation at random (upwards or downwards, \( s_i = \pm 1/2 \)) independently of nearby spins. When we have really long spin lattice, \( N\rightarrow \infty \), central limit theorem starts to be applicable and the distribution of magnetization, \( M = \sum_i s_i \), starts to approach Gaussian:

\begin{equation} P_{nc}(M) = \frac{1}{2^N} \frac{N!}{(M+N/2)!(N/2-M)!} \sim\exp\left(-\frac{2 M^2}{N}\right) . \label{gauss} \end{equation}

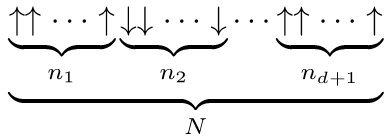Fig. 1:Illustration of the correlated spin model taken from the article.

Now let us assume that our spins are strongly correlated. This means that there is only a few cases when spins change orientation. Let us assume that there is \( d \) such cases, with \( d \ll N \). In such case we have \( d+1 \) single spin orientation domains. Consequently in this case we can rewrite the global magnetization as:

\begin{equation} M = s_1 \sum_{i=1}^{d+1} (-1)^{i-1} n_i , \end{equation}

where \( s_1 \) is orientation of the first spin, \( n_i \) is the size \( i \)-th domain. Now the distribution of \( M \) is no longer Gaussian (unless \( d \gg 1 \)), it is well approximated by power-law [1]:

\begin{equation} P_{c}(M) \propto \left(1-\frac{4M^2}{N^2}\right)^{\mathrm{int}\left[\frac{d-1}{2}\right]} ,\label{laips} \end{equation}

here \( \mathrm{int}[x] \) extracts integer part of a real number (fractional part is dropped). It should be evident that \( P_{c}(M) \) can be rewritten using q-Gaussian with \( q = 1 -\mathrm{int}\left[\frac{d-1}{2}\right]^{-1} \). We invite you to check this using our interactive applets.

Applets

First applet is dedicated to generation of single instances of random lattices and their magnetization, \( M \). Red color in this applet denotes spins directed upwards, while blue - spins directed downwards. To simplify this applet we have fixed number of spins in the lattice, \( N \), but you can still manipulate \( d \).

The second applet, on the other hand, is dedicated to mass generation of random magnetization. Use this applet to check how well modelic PDF agrees with theoretical ones, \eqref{gauss} and \eqref{laips}. Note that when \( d \) is small, then power-law approximation, \eqref{laips}, works well, but when \( d \) grows the exponential approximation starts to fit better, \eqref{gauss}.

References

• J. Ruseckas. Probabilistic model of N correlated binary random variables and non-extensive statistical mechanics. Physics Letters A 379: 654-659 (2015). doi: 10.1016/j.physleta.2014.12.038. arXiv: 1408.0088v2 [cond-mat.stat-mech].