Multi-success detrapping process

When presenting heterogeneous detrapping process at the DPG conference I got a question (or a suggestion to check) what would happen if instead of heterogeneous traps we would require multiple successes for the charge carrier to escape?

Erlang distributed detrapping times

If we require the charge carrier to make \( N_{success} \) successful "escapes" before actually escaping the trap, and each individual escape times are sampled from exponential distribution (with rate given by \( \lambda_\tau \)), then the overall detrapping time will follow Erlang distribution with \( k = N_{success} \) and \( \lambda = \lambda_\tau \).

Probability density function of the Erlang distribution is given by

\begin{equation} p(\tau) = \frac{\lambda^{k}}{(k-1)!} \tau^{k-1} \exp(-\lambda \tau). \end{equation}

Observe that the asymptotic behavior of this probability density function is exponential. I.e., for extremely large \( \tau \), we have that \( p(\tau) \sim \exp(-\lambda \tau) \). Which leads us to predict that nothing interesting will happen - the power spectral density should remain almost the same as predicted in the earlier post.

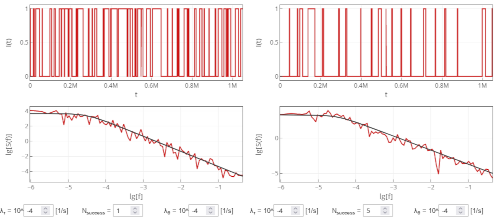Fig. 1:Comparison between one-success and multi-success signals and PSDs.

When running the simulations on the interactive app below we see that larger \( N_{success} \) decreases the number of pulses in the observed signal. This leads to slightly smaller signal power spectral density, but does not induce other effects.

Interactive app

This app is identical to the one presented in an earlier post, but now you are encouraged to verify insights of this posts by changing \( N_{success} \) parameter values.