Power-law gap times in random telegraph noise

In the last post we have assumed that the event rate of the individual processes making up the superposition needs to be distributed according the bounded Pareto distribution. And we have seen that in \( \alpha = 0 \) case, 1/f noise will be obtained. But superposition of such processes seems to be very demanding assumption, maybe we can choose another assumption? Here we will see what happens if we assume that gap times are assumed to follow bounded Pareto distribution, while the pulse times will still follow exponential distribution.

What if the gaps are power-law distributed?

Recall that here we consider a signal, which is composed of non-overlapping rectangular pulses (see Fig. 1). Thus it is full described by a sequence of gap (detrapping) times, \( \tau_i \), and pulse (trapping) times, \( \theta_i \).

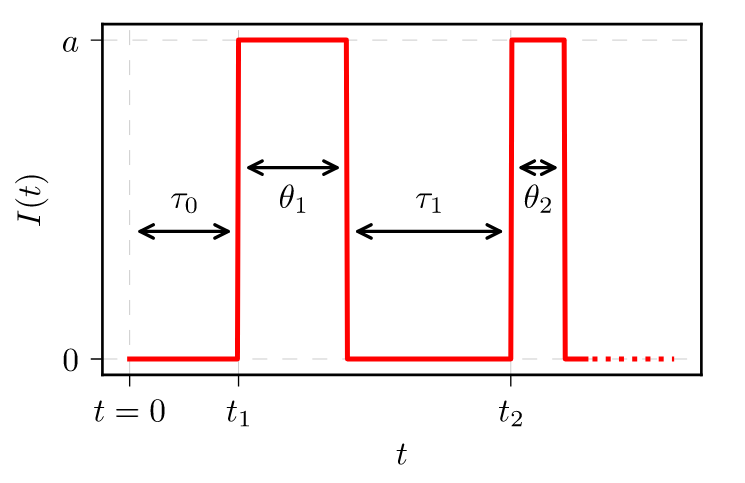Fig. 1:Fragment of a signal with non-overlapping rectangular pulses.

In an earlier post we have assumed that both \( \tau_i \) and \( \theta_i \) are sample from the same exponential distribution and have obtained Lorentzian spectral density. But let us now use the general result from [1],

\begin{equation} S\left(f\right)=\frac{a^{2}\bar{\nu}}{\pi^{2}f^{2}}\mathrm{Re}\left[\frac{\left(1-\chi_{\theta}\left(f\right)\right)\left(1-\chi_{\tau}\left(f\right)\right)}{1-\chi_{\theta}\left(f\right)\chi_{\tau}\left(f\right)}\right], \label{eq:general-result} \end{equation}

to derive the spectral density when \( \tau_i \) are sample from the bounded Pareto distribution. We already know that characteristic function for the exponential distribution (which in our case is the pulse duration distribution) is given by

\begin{equation} \chi_{\theta}(f) = \frac{\lambda_{\theta}}{\lambda_{\theta} - 2 \pi \mathrm{i} f} = \frac{1}{1-2 \pi \mathrm{f} \mathrm{i} \theta_c} \end{equation}

Where in the above \( \theta_c \) is the average pulse duration (i.e., \( \theta_c = \langle \theta \rangle = \frac{1}{\lambda_{\theta}} \)).

In this post we assume that gap times are sampled from the bounded Pareto distribution, whose probability density function would be given by:

\begin{equation} p\left(\tau\right)= \begin{cases} \frac{\alpha\tau_{\text{min}}^{\alpha}}{1-\left(\frac{\tau_{\text{min}}}{\tau_{\text{max}}}\right)^{\alpha}}\cdot\frac{1}{\tau^{\alpha+1}} & \text{for }\tau_{\text{min}}\leq\tau\leq\tau_{\text{max}},\\ 0 & \text{otherwise}. \end{cases} \end{equation}

In the above, by the usual convention, \( \alpha > 0 \). The characteristic function of this distribution is then given by

\begin{equation} \chi_{\tau}\left(f\right)=\frac{\alpha\left(-2\pi\mathrm{i} f\tau_{\text{min}}\tau_{\text{max}}\right)^{\alpha}}{\tau_{\text{max}}^{\alpha}-\tau_{\text{min}}^{\alpha}}\cdot\left[\Gamma\left(-\alpha,-2\pi\mathrm{i} f\tau_{\text{min}}\right)-\Gamma\left(-\alpha,-2\pi\mathrm{i} f\tau_{\text{max}}\right)\right]. \end{equation}

Which is somewhat more complicated, thus let us approximate it for \( 0 < \alpha < 2 \) with a notable exception of \( \alpha = 1 \) and for \( \frac{1}{2\pi\tau_{\text{max}}}\ll f\ll\frac{1}{2\pi\tau_{\text{min}}} \):

\begin{equation} \chi_{\tau}\left(f\right) \approx 1+\frac{\alpha}{\alpha-1}\cdot\left(2\pi\mathrm{i} f\tau_{\text{min}}\right)-\Gamma\left(1-\alpha\right)\cdot\left(-2\pi\mathrm{i} f\tau_{\text{min}}\right)^{\alpha}. \end{equation}

Inserting the above characteristic functions into Eq. \eqref{eq:general-result} yields

\begin{equation} S\left(f\right)=\frac{4a^{2}\bar{\nu}\theta_{c}^{2}\left(2\pi f\tau_{\text{min}}\right)^{\alpha}\cos\left(\frac{\pi\alpha}{2}\right)\Gamma\left(1-\alpha\right)}{\frac{4\pi^{2}f^{2}}{\left(\alpha-1\right)^{2}}\left[\left(\alpha-1\right)\theta_{c}+\alpha\tau_{\text{min}}\right]^{2}+\left(2\pi f\tau_{\text{min}}\right)^{2\alpha}\Gamma\left(1-\alpha\right)^{2}}.\label{eq:full-psd} \end{equation}

This expression is still rather complicated and hard to understand. What we done in [1] is that we considered its asymptotic behavior in limiting cases. First in [1] we have considered short pulse duration case, i.e., \( \theta_c \ll \tau_{\text{min}} \), which in the extreme scenario should be equivalent to a point process (we have already discussed this in an earlier post). In we have confirmed that for \( 0 < \alpha < 1 \):

\begin{equation} S(f) \sim \frac{1}{f^\alpha} , \end{equation}

and for \( 1 < \alpha < 2 \):

\begin{equation} S(f) \sim \frac{1}{f^{2-\alpha}} . \end{equation}

This peculiar behavior arises, because different terms dominate in the denominator of Eq. \eqref{eq:full-psd}. For \( 0 < \alpha < 1 \), the term involving \( f^{2\alpha} \) is the most significant of the two terms in the denominator. While for confirmed that for \( 1 < \alpha < 2 \) it is easy to see that \( f^2 \) term dominates.

This peculiarity disappears if we consider long pulse duration case, i.e., \( \theta_c \gg \tau_{\text{min}} \). Then, for all non-integer \( \alpha \), \( f^2 \) term dominates. So for the long pulse duration case we have that:

\begin{equation} S(f) \sim \frac{1}{f^{2-\alpha}} . \end{equation}

These results suggest that for \( \alpha = 1 \) we should observe 1/f noise, and in the existing literature it was so assumed. But as we have seen in an earlier post), for the extremely short pulses no 1/f noise is observed - the dependence is perverted by the presence \( \ln f \) term.

The special case of \( \alpha = 1 \)

With \( \alpha = 1 \), and for \( \frac{1}{2\pi\tau_{\text{max}}}\ll f\ll\frac{1}{2\pi\tau_{\text{min}}} \), we have the following expression for the characteristic function of gap time distribution

\begin{equation} \chi_{\tau}\left(f\right)=1-\pi^{2}f\tau_{\text{min}}+\left[1-C_{\gamma}-\ln\left(2\pi f\tau_{\text{min}}\right)\right]\cdot\left(2\pi\mathrm{i} f\tau_{\text{min}}\right).\label{eq:pareto-char-a1} \end{equation}

Where, in the above, \( C_{\gamma}=0.577\ldots \) is the Euler's gamma constant. Inserting Eq. \eqref{eq:pareto-char-a1} into Eq. \eqref{eq:general-result} yields

\begin{equation} S\left(f\right)=\frac{a^{2}\bar{\nu}\tau_{\text{min}}}{\left(\frac{\pi\tau_{\text{min}}}{2\theta_{c}}\right)^{2}+\left\{ 1+\frac{\tau_{\text{min}}}{\theta_{c}}\left[1-C_{\gamma}-\ln\left(2\pi\tau_{\text{min}}f\right)\right]\right\}^{2}}\cdot\frac{1}{f}. \end{equation}

It should be evident that, if the pulses are short, then \( \ln f \) term is significant. On the other hand, if the pulses are long, then for the most parameters sets and realistically measurable frequencies pure 1/f noise is obtained

\begin{equation} S\left(f\right) \approx a^{2}\bar{\nu}\tau_{\text{min}}\cdot\frac{1}{f}. \end{equation}

Still, if we consider all frequencies (or the formal mathematical \( f \rightarrow 0 \) limit), then the obtained 1/f noise would be still perverted by the \( \ln f \) term. Though the cutoff frequency would most often be unrealistically low:

\begin{equation} f^{\left(c\right)}=\frac{1}{2\pi\tau_{\text{min}}}\exp\left[-\left(\sqrt{2}-1\right)\frac{\theta_{c}}{\tau_{\text{min}}}\right]. \end{equation}

If put the values used in the article [1] or the app below, then we get that \( f^{\left(c\right)}\approx10^{-180} \). Measuring power spectral density up to such frequency is nearly impossible. This effectively offers an alternative resolution to the low-frequency cutoff paradox [2].

What does this model has to do with either \( f \rightarrow 0 \) limit or the low-frequency cutoff paradox? Well, you can always take the \( \tau_{max} \rightarrow \infty \) limit. In simulation you would set \( \tau_{max} \) value much larger than the observation time (experiment duration). This makes the model weakly non-ergodic and induces aging effects. Namely, the total power of a signal (obtained by integrating the spectral density over observed frequencies) decays as the observation time increases. For \( \alpha = 1 \) case, which leads to 1/f noise, this decay is extremely slow, approximately

\begin{equation} \int_{1/T}^\infty S(f) \mathrm{d}f \propto \frac{1}{\ln(T)} . \end{equation}

You won't be able to observe it unless you are actively looking for the signs of the decrease. More details on the weakly non-ergodic case and the exhibited aging effects are presented in [1].

Interactive app

This interactive app is somewhat similar to the app generating Lorentzian spectral density (see this post). The key difference is that here the app doesn't generate a single time series of predefined length when the "Generate" button is pressed. Instead it generates time series (and calculates the spectral density continuously until the "Stop" button is pressed. When "Generate" button is pressed again, the parameters are reset and the generation of new time series is started.

What to observe? You might want to try changing \( \theta_c \) and observe how the apparently pure 1/f noise disappears. Also you might want to change \( \alpha \) to observe the different slopes that can emerge from this model.

References

• A. Kononovicius, B. Kaulakys. 1/f noise from the sequence of nonoverlapping rectangular pulses. Physical Review E 107: 034117 (2023). doi: 10.1103/PhysRevE.107.034117. arXiv:2210.11792 [cond-mat.stat-mech].
• M. Niemann, H. Kantz, E. Barkai. Fluctuations of 1/f noise and the low-frequency cutoff paradox. Physical Review Letters 110: 140603 (2013). doi: 10.1103/PhysRevLett.110.140603.