Replacement model of dating apps

In this post I continue my exploration of the [1]. This time let us consider what happens if the users who were matched are replaced by a random sample from the population. Will only the least and most attractive ones remain unmatched?

Replacement model

The replacement model is a logical extension of the dropout model. In this variation of the original model the agents who were matched are replaced by other new agents. The new agents are sampled from the same distribution from which initial population of agents was sampled.

As we have seen in the earlier post the most attractive agents weren't the most matched agents. In fact, average agents were matched the most. So, based on this observation we would expect that least and most attractive agents would search for the match longer than the average users. Yet numerical simulation would indicate that this expectation is at least partially wrong.

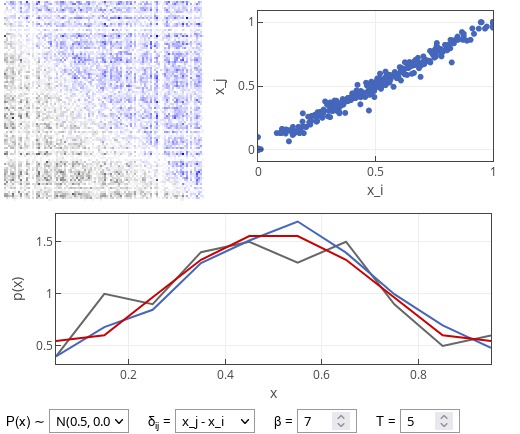Fig 1.(lower figure) Comparison sample population (red curve), matched user population (blue curve) and the active user population (grey curve) match.

As we can see in the figure above three groups have similar distributions, although the active user attractiveness distribution seems to fluctuate a lot. One of the reasons is that there are just a relatively few active users (those using the dating app). Though I would speculate that there is another reason for the observed fluctuations - left-over extreme users.

Interactive app

This app is essentially identical to the one from the previous posts. The only addition is the replacement mechanism. Feel free to explore!

References

• F. Olmeda. Towards a statistical physics of dating apps. arXiv:2107.14076 [physics.soc-ph].