Standing ovation model

It has been a long time since last interactive model on Physics of Risk. This time we return to a problem we have already previously considered, but which we did not model.

From time to time almost everyone of us has an opportunity to go see a play. Afterwards everyone has to make a choice - to applaud or not to. It appears to be free choice, but actually it isn't as there are various social feedback loops in play. This problem was considered as a simple agent-based model in a paper by Miller and Page [1]. In this text we will briefly introduce you to it.

The model

Imagine we have a square auditorium of certain size (it is adjustable in the app below). All of the chair in the auditorium are taken by agents, who have to decide to join standing ovation (green) or not to (red). Of course in real world people would eventually leave the auditorium (and ones who have not liked the play earlier), but for the sake of simplicity we assume that agents do not leave the auditorium.

Initial agent's decision is determined solely by how much the agent likes the play. This "likeability" is an internal parameter, which differs for all agents and which is drawn from uniform distribution (restricted in \( [0,1] \)). Yet the stand up threshold is a global model parameter, \( T \). The larger \( T \), the less agents will stand up. The internal "likeability," in the app below is shown by adjusting luminosity of the colors (the darker the color is, the less agent likes the play).

But the "likeability" matters only during the first step. Afterwards each agents looks at his neighbors. If the agent sees that majority of his neighbors do the opposite thing, then to avoid feeling uncomfortable he will change his behavior. Namely if majority of neighbors are applauding, then the agent will also join applause. If majority of neighbors are sitting silently, then he will also sit. The model has an important catch - one agent can see only limited amount of other agents. His field of view is limited (see figure below).

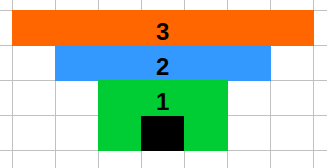Fig 1.Agent's field of view is a cone. Vision radius is a choosable model parameter (cases up until r=3 are shown).

Here we would like to draw your attention to one slightly unrealistic assumption we have made. Our auditorium uses periodic boundary conditions (alternatively, it is a torus). Namely agents sitting in front see the agents sitting in the back. Ones sitting leftmost see the agents sitting rightmost. While it is impossible in reality, this assumption is common in physics to avoid "boundary effects".

Also we would like to note that in our implementation agents update their behavior synchronously.

The dynamics

Using the same parameter set \( T=0.5 \) and \( r=1 \) we have reproduced all possible outcomes of the model - whole auditorium ovation, periodic ovation and silent auditorium.

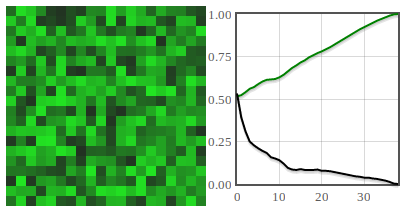Fig 2.After some time all agents have joined standing ovation (green curve is at 1). No agents feel uncomfortable (black curve is at 0).

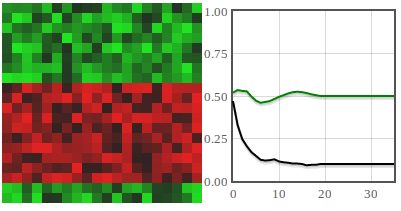Fig 3.Periodic ovation has developed. Agents stand up and after some time sit down. A fraction of agents remains uncomfortable.

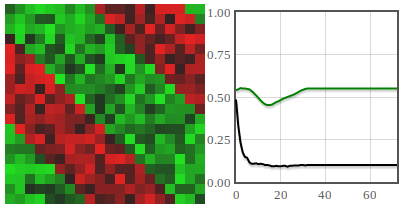Fig 4.Periodic ovation has developed. Agents stand up and after some time sit down. A fraction of agents remains uncomfortable. The main difference from the previous example is a shape of the 'front.'

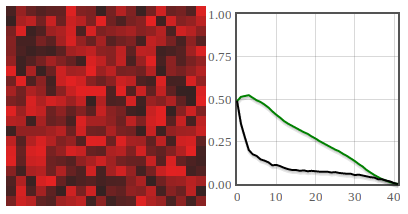Fig 5.After some time applause dies down (green curve is at 0). No agents feel uncomfortable (black curve is at 0).

Interactive HTML5 applet

Below you should see an interactive HTML5 app, which uses the algorithm described above. Model parameters and curves shown in the figure were discussed in the text. Try different parameter values for yourself to understand their importance to the observed dynamics of the model.

References

• J. H. Miller, S. E. Page. The standing ovation problem. Complexity 9: 8-16 (2004). doi: 10.1002/cplx.20033.