The illogical world - nontransitive dice

Previously we wrote about the "illogical" world, which is full of paradoxes and nontransitivity. This time we discuss an elementary dice game, which is also nontransitive and thus appears to be unnatural, "cheated" and etc. Yet the example is completely natural and easily understandable, it can be also tested empirically (and not only theoretically as the previous example) - it can be played at home! All of the relevant information you'll hear in the youtube video (see below).

We also provide a more simple take on the same topic below.

Transitivity is natural and expected property. It is how the most of the times "it should be". For example, it is clearly understandable that if 10 is larger than 7 and 7 is larger than 5, then 10 is also larger than 5. The properties are "inherited" in a transparent fashion. Yet life itself is not that simple and transparent. Previously we have already given example on the preference chain, which can indeed become a cycle. This purely theoretical example can also be experience empirically by making the dice as they are show in the figure (note that the walls, which are not seen, mirror values shown on the walls, which are seen). Which of the dice is a better one? Which one will roll higher values than the other two?

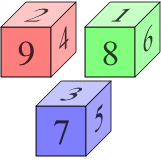Fig 1.Nontransitive dice. Image taken from Wikipedia

The answer should be evident - the red one will beat the green one with the probability of 5/9, the green one will be better than blue one with the probability of 5/9. Now, naturally one would expect that the red die should be better than the blue die, but it is not so. The blue die wins against red one with the probability of 5/9! How that can be? Note the values on the dice!

Applet

Would you like to try to defeat opponent who always selects the superior die? Go ahead and try! Note that after playing many games your opponent gains upper hand.