Total population dynamics in the compartmental voter model

Today we continue our series of posts on compartmental voter model. Recently I had another idea how to examine the impact of the finite capacity on the compartmental voter model dynamics. And this approach also involves populations dynamics in the model.

For a different approach see the earlier post on the finite capacity in the compartmental voter model.

The app we make available with this post is quite similar to the one from the earlier post, but this one is different as we report distinct quantities: total number of agents in the compartment (blue dots) and scaled number of agents of the first type (red dots). We report spatial rank-size distributions for both of them.

If capacity would have no impact on the model dynamics, then both observables would have similar rank-size distributions and the curves would noticeably overlap.

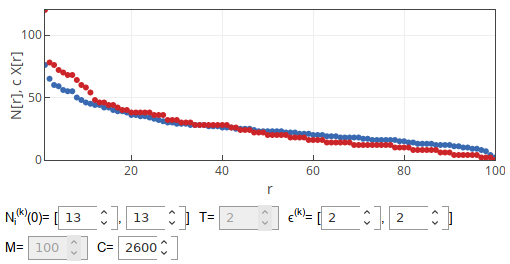Fig. 1:We can see that capacity does not have influence on the dynamics if it is infinite.

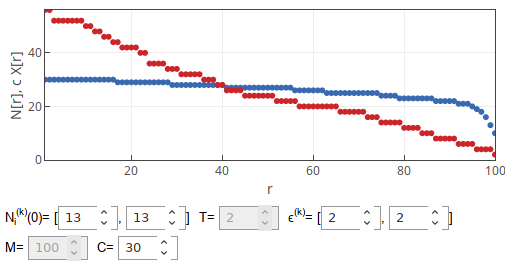Fig. 2:We can see that capacity does have influence if it is finite.

Interactive app

As always, feel free to explore on your own!

Acknowledgment. This post is based on research which was carried out as a part of the postdoctoral fellowship ''Physical modeling of order-book and opinion dynamics'' (09.3.3-LMT-K-712-02-0026) project. The fellowship is funded by the European Social Fund under the No 09.3.3-LMT-K-712 ''Development of Competences of Scientists, other Researchers and Students through Practical Research Activities'' measure.