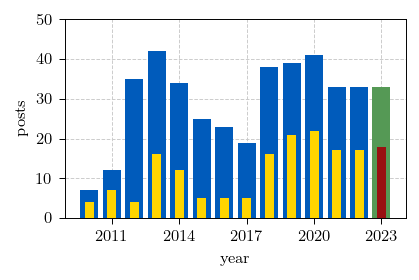
Over the last few years we have been keeping a steady pace of 33 posts a
year. Though in 2023 we have managed to produce one more post containing
an interactive app.
This year we have mostly focused on the various properties of Poisson
processes and related topics (such as point
processes and shot noise).
Otherwise we have finished a series of posts from the 2022 on the
statistical modeling of dating apps.
There were also some major changes "under the hood". First of all we have
moved from local server, which was managed by ourselves, to GitHub Pages.
When making transition we have noticed couple of issues. Most immediate
issues are already resolved. For example, some of the links were broken, or
not using common practices in Pelican. Some of the less important issues,
which can be easily fixed, were fixed. For example, we have renamed numerous
article files in the source repository so that their names would match
article slugs. What remains, is to fix some figure file names (also to match
respective article slugs and the content of the figure). Also, as the number
of interactive apps is growing every year, it seems worthwhile to reorganize
their code in the source repository by putting them in "thematic"
directories (for example, based on research topic or model type).
What is coming in 2024? Well, most likely we will have few more posts
dedicated to our recent works on the random telegraph
noise. Then I will likely tell you about my
woes with football themed board game
Eleven.
While it is highly thematic, it has some glaring issues which I wanted to
fix with science! Well, numerical simulation at least.