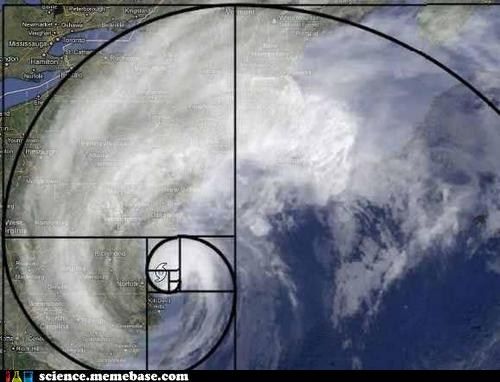
Hurricane Sandy
Recent hurricane, which struck east coast of the USA, has very interesting symmetry properties. This natural phenomenon obeys the golden ratio! Well at least such information has been circulating on the science.memebase.com! Similar properties are also observed in some fractals such as Penrose tiling (we have not yet discussed this fractal on Physics of Risk, thus we'd like to recommend reading an article on the Wikipedia).